
| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{2}$ | D. | 2 |
分析 与(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$),可得(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=0.可得:$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=$\frac{1}{4}$.再利用数量积运算性质即可得出.
解答 解:∵(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$),∴(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=-4${\overrightarrow{{e}_{1}}}^{2}$+3${\overrightarrow{{e}_{2}}}^{2}$+4$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=-1+4$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=0.
可得:$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=$\frac{1}{4}$.
则|$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$|=$\sqrt{{\overrightarrow{{e}_{1}}}^{2}+4{\overrightarrow{{e}_{2}}}^{2}+4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}$=$\sqrt{1+4+4×\frac{1}{4}}$=$\sqrt{6}$.
故选:A.
点评 本题考查了向量垂直与数量积的关系、数量积运算性质,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
 如图,AB=38米,从点A发出的光线经水平放置于C处的平面镜(大小忽略不计)反射后过点B,已知AC=10米,BC=42米.
如图,AB=38米,从点A发出的光线经水平放置于C处的平面镜(大小忽略不计)反射后过点B,已知AC=10米,BC=42米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
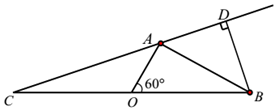 随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;
随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com