
 如图所示的三棱锥P-ABC中,∠BAC=90°,PA⊥平面ABC,AB=AC=2,PA=4,E,F,G分别为棱PB,BC,AC的中点,点H在棱AP上,AH=1.
如图所示的三棱锥P-ABC中,∠BAC=90°,PA⊥平面ABC,AB=AC=2,PA=4,E,F,G分别为棱PB,BC,AC的中点,点H在棱AP上,AH=1.分析 (1)以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能推导出$\overrightarrow{EG}$与$\overrightarrow{PA}$$+\overrightarrow{BC}$共线.
(2)点H在棱AP上,AH=1,得H(0,0,1),利用向量法求出$\overrightarrow{HE}$⊥$\overrightarrow{HF}$,从而S△HEF=$\frac{\sqrt{6}}{2}$,出平面HEF的法向量$\overrightarrow{n}$=(1,-2,-1),从而点G到平面HEF的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{HG}|}{|\overrightarrow{n}|}$=$\frac{1}{\sqrt{6}}$=$\frac{\sqrt{6}}{6}$,由此能求出空间四面体EFGH的体积.
解答  解:(1)∵三棱锥P-ABC中,∠BAC=90°,PA⊥平面ABC,
解:(1)∵三棱锥P-ABC中,∠BAC=90°,PA⊥平面ABC,
∴以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,
∵AB=AC=2,PA=4,E,F,G分别为棱PB,BC,AC的中点,
∴A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,4),E(1,0,2),G(0,1,0),
$\overrightarrow{EG}$=(-1,1,-2),$\overrightarrow{PA}$=(0,0,-4),$\overrightarrow{BC}$=(-2,2,0),
∴$\overrightarrow{PA}+\overrightarrow{BC}$=(-2,2,-4)=2(-1,1,-2)=2$\overrightarrow{EG}$,
∴$\overrightarrow{EG}$与$\overrightarrow{PA}$$+\overrightarrow{BC}$共线.
(2)∵点H在棱AP上,AH=1,∴H(0,0,1),F(1,1,0),
$\overrightarrow{HE}$=(1,0,1),$\overrightarrow{HF}$=(1,1,-1),$\overrightarrow{HG}$=(0,1,-1),
∵$\overrightarrow{HE}•\overrightarrow{HF}$=1+0-1=0,∴$\overrightarrow{HE}$⊥$\overrightarrow{HF}$,
∴S△HEF=$\frac{1}{2}×|\overrightarrow{HE}|×|\overrightarrow{HF}|$=$\frac{1}{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{6}}{2}$,
设平面HEF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{HE}=x+z=0}\\{\overrightarrow{n}•\overrightarrow{HF}=x+y-z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-2,-1),
点G到平面HEF的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{HG}|}{|\overrightarrow{n}|}$=$\frac{1}{\sqrt{6}}$=$\frac{\sqrt{6}}{6}$,
∴空间四面体EFGH的体积:
V=VG-HEF=$\frac{1}{3}×{S}_{△HEF}×d$=$\frac{1}{3}×\frac{\sqrt{6}}{2}×\frac{\sqrt{6}}{6}$=$\frac{1}{6}$.
点评 本题考查两向量是否共线的判断与证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、考查函数与方程思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2n+1-2 | B. | 3n | C. | 2n | D. | 3n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ先变小再变大 | B. | 当M为线段BC中点时,λ最大 | ||
| C. | λ先变大再变小 | D. | λ是一个定值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α∥β | B. | α⊥β | ||
| C. | α,β相交但不垂直 | D. | α,β所成的锐二面角为60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB=38米,从点A发出的光线经水平放置于C处的平面镜(大小忽略不计)反射后过点B,已知AC=10米,BC=42米.
如图,AB=38米,从点A发出的光线经水平放置于C处的平面镜(大小忽略不计)反射后过点B,已知AC=10米,BC=42米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
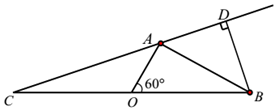 随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;
随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com