
分析 (1)由题意利用诱导公式化简所给的三角函数式,可得结果.
(2)利用同角三角函数的基本关系求得sinα、cosα的值,可得sinα-cosα的值.
解答 解:(1)sin2120°+cos180°+tan45°-cos2(-330°)+sin(-210°)
=sin260°+cos180°+tan45°-cos230°+sin150°
=${(\frac{{\sqrt{3}}}{2})^2}-1+1-{(\frac{{\sqrt{3}}}{2})^2}+\frac{1}{2}$=$\frac{1}{2}$.
(2)∵$tanα=\sqrt{3},且π<α<\frac{3}{2}π$,∴sinα<0,cosα<0,
由$\left\{\begin{array}{l}sinα=\sqrt{3}cosα\\{sin^2}α+{cos^2}α=1\end{array}\right.$ 解得$\left\{\begin{array}{l}sinα=-\frac{{\sqrt{3}}}{2}\\ cosα=-\frac{1}{2}\end{array}\right.$,∴$sinα-cosα=\frac{{1-\sqrt{3}}}{2}$.
点评 本题主要考查应用同角三角函数的基本关系、诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
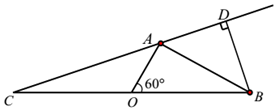 随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;
随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有A,B,C三个旅游景点,在岸边BC两地的中点处设有一个垃圾回收站点O(如图),A,B两地相距10km,从回收站O观望A地和B地所成的视角为60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,设AC=xkm;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com