
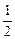 ],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0. 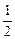 )、f(
)、f(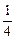 );
);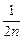 ),求
),求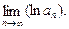
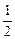 )=a
)=a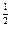 , f(
, f(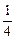 )=a
)=a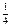 (2) 证明略(3)
(2) 证明略(3)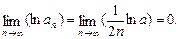
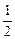 ],都有f(x1+x2)=f(x1)·f(x2),所以f(x)=
],都有f(x1+x2)=f(x1)·f(x2),所以f(x)=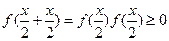 , x∈[0,1]
, x∈[0,1]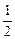 +
+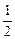 )=f(
)=f(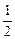 )·f(
)·f(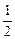 )=[f(
)=[f(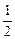 )]2
)]2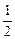 )=f(
)=f(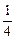 +
+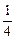 )=f(
)=f(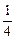 )·f(
)·f(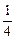 )=[f(
)=[f(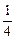 )]2
)]2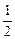 )=a
)=a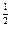 , f(
, f(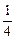 )=a
)=a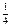

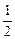 )=f(n·
)=f(n·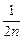 )=f(
)=f(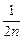 +(n-1)
+(n-1)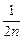 )=f(
)=f(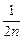 )·f((n-1)·
)·f((n-1)·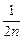 )=……
)=……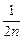 )·f(
)·f(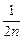 )·……·f(
)·……·f(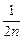 )
)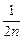 )]n=a
)]n=a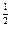
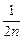 )=a
)=a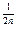 .
.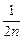 )=f(
)=f(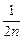 ),
), 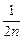 )=f(
)=f(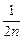 )=a
)=a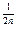 .
.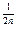
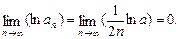


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
 ,g(x)=
,g(x)= .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
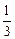 ),f(
),f(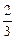 ),f(1)的大小关系_________.
),f(1)的大小关系_________. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com