
分析 由题意可得数列{$\frac{1}{{a}_{n}}$}是以1为首项的等差数列,再求出公差d,即可求得an.
解答 解:∵a1=1,
∴$\frac{1}{{a}_{1}}$=1,
∵$\frac{2}{{a}_{n}}$=$\frac{1}{{a}_{n+1}}+\frac{1}{{a}_{n-1}}$(n≥2),
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项的等差数列,
∵a5=-11,
∴$\frac{1}{{a}_{5}}$=-$\frac{1}{11}$,
设数列{$\frac{1}{{a}_{n}}$}的公差为d,
∴$\frac{1}{{a}_{5}}$=$\frac{1}{{a}_{1}}$+4d,
∴-$\frac{1}{11}$=1+4d,
解得d=-$\frac{3}{11}$,
∴$\frac{1}{{a}_{n}}$=1-$\frac{3}{11}$(n-1),
∴an=$\frac{11}{14-3n}$,
当n=1时,a1=1成立,
综上所述其通项为an=$\frac{11}{14-3n}$,( n∈N+ )
故答案为:an=$\frac{11}{14-3n}$,( n∈N* )
点评 本题主要考查用构造法求数列的通项公式,判断数列{$\frac{1}{{a}_{n}}$}是以1为首项的等差数列是解题的关键,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图,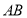 是
是 的直径,
的直径,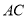 是
是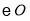 的切线,
的切线, 交
交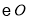 于点
于点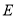 .
.
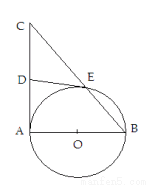
(1)过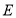 做
做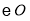 的切线,交
的切线,交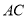 与点
与点 ,证明:
,证明: 是
是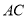 的中点;
的中点;
(2)若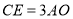 ,求
,求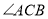 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年重庆市高二上学期入学考试数学试卷(解析版) 题型:解答题
△ABC中内角A,B,C的对边分别为a,b,c,向量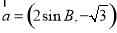 ,
, 且
且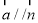 .
.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积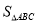 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com