
���� ��1�����ֱ��l��x��Ľ��㣬�ɵ�c=2��������ֱ��ƽ�е�������б����ȣ��ɵý����߷��̣��ⷽ�̿ɵ�a��b�������õ�˫���ߵķ��̣�
��2����ֱ��y=kx+1��k��0��������$\frac{{x}^{2}}{3}$-y2=1�ɵã���1-3k2��x2-6kx-6=0����M��x1��y1����N��x2��y2��������Τ�ﶨ�����б�ʽ����0���Լ��е����깫ʽ����ֱ�ߴ�ֱ��������б��֮��Ϊ-1�����MN�Ĵ�ֱƽ���߷��̣���x=0���ɵ�ֱ����y���ϵĽؾ࣬�ɲ���ʽ�����ʿɵ÷�Χ��
��� �⣺��1��ֱ��l��y=$\frac{\sqrt{3}x}{3}$-$\frac{2\sqrt{3}}{3}$��x����һ�㣨2��0����
������ɵ�c=2����a2+b2=4��
˫���ߵĽ����߷���Ϊy=��$\frac{b}{a}$x��
����ֱ��ƽ�е������ɵ�$\frac{b}{a}$=$\frac{\sqrt{3}}{3}$��
���a=$\sqrt{3}$��b=1��
����˫���ߵķ���Ϊ$\frac{{x}^{2}}{3}$-y2=1��
��2����ֱ��y=kx+1��k��0����
����$\frac{{x}^{2}}{3}$-y2=1�ɵã���1-3k2��x2-6kx-6=0��
��M��x1��y1����N��x2��y2����
x1+x2=$\frac{6k}{1-3{k}^{2}}$��x1x2=$\frac{6}{3{k}^{2}-1}$��
MN�е�Ϊ��$\frac{3k}{1-3{k}^{2}}$��$\frac{1}{1-3{k}^{2}}$����
�ɵ�MN�Ĵ�ֱƽ���߷���Ϊy-$\frac{1}{1-3{k}^{2}}$=-$\frac{1}{k}$��x-$\frac{3k}{1-3{k}^{2}}$����
��x=0���ɵ�y=$\frac{4}{1-3{k}^{2}}$��
�ɡ�=36k2+24��1-3k2����0�����3k2��2��
��$\frac{6}{3{k}^{2}-1}$��0�����3k2��1��
���Ͽɵã�0��3k2��1��
����$\frac{4}{1-3{k}^{2}}$�ķ�Χ�ǣ�4��+�ޣ���
�ɵ�ֱ��m��y���ϵĽؾ��ȡֵ��ΧΪ��4��+�ޣ���
���� ���⿼��˫���ߵķ��̵���ע������ֱ����x��Ľ������ֱ��ƽ�е�����������ֱ�߷��̺�˫���߷�������������Τ�ﶨ�����е����깫ʽ���Լ���ֱ�ߴ�ֱ��������б��֮��Ϊ-1�����黯�����������������������е��⣮


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��+�ޣ� | B�� | ��0��1�� | C�� | ��1��$\sqrt{2}$] | D�� | ��-1��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1 | B�� | $��\frac{2}{3}$ | C�� | $��\frac{1}{3}$ | D�� | $��\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�������и߶���ѧ����ѧ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��{1,2,3,4,5}�����ѡȡһ����Ϊa����{1,2,3}�����ѡȡһ����Ϊb����b>a�ĸ����ǣ� ��
A.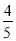 B.
B.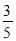 C.
C.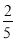 D.
D.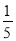
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com