
分析 建立坐标系,设P(2cosθ,sinθ),求出$\overrightarrow{PA},\overrightarrow{PB}$的坐标,代入数量积公式得到关于θ的三角函数,利用正弦函数的性质得出.
解答  解:以三角形的外接圆圆心为原点建立平面直角坐标系.
解:以三角形的外接圆圆心为原点建立平面直角坐标系.
设A(2,0),B(-1,$\sqrt{3}$),P(2cosθ,2sinθ).
则$\overrightarrow{PA}$=(2cosθ-2,2sinθ),$\overrightarrow{PB}$=(2cosθ+1,2sinθ-$\sqrt{3}$).
∴$\overrightarrow{PA}•\overrightarrow{PB}$=(2cosθ-2)(2cosθ+1)+2sinθ(2sinθ-$\sqrt{3}$)
=2-2cosθ-2$\sqrt{3}$sinθ
=2-4sin(θ+$\frac{π}{6}$).
∴-2≤$\overrightarrow{PA}•\overrightarrow{PB}$≤6.
故答案为[-2,6].
点评 本题考查了平面向量的数量积运算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
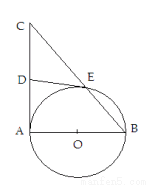
如图,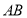 是
是 的直径,
的直径,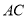 是
是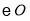 的切线,
的切线, 交
交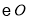 于点
于点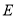 .
.
(1)过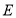 做
做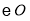 的切线,交
的切线,交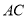 与点
与点 ,证明:
,证明: 是
是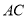 的中点;
的中点;
(2)若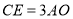 ,求
,求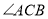 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com