
分析 (1)根据平面向量的共线定理,列出方程求出tanx的值;
(2)根据平面向量的数量积求出f(x),再利用正弦函数的单调性求出f(x)的单调增区间.
解答 解:(1)由$\overrightarrow{m}$∥$\overrightarrow{n}$得:sin(x-$\frac{π}{6}$)-cosx=0,
展开变形可得:$\frac{\sqrt{3}}{2}$sinx-$\frac{3}{2}$cosx
∴sinx=$\sqrt{3}$cosx,
即tanx=$\sqrt{3}$;…(6分)
(2)f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=$\frac{1}{2}$sin(2x-$\frac{π}{6}$)+$\frac{3}{4}$,
由-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z得:
$-\frac{π}{6}+kπ≤x≤\frac{π}{3}+kπ,k∈Z$;
又因为x∈[0,π],
所以x∈[0,π]时,f(x)的单调增区间为[0,$\frac{π}{3}$]和[$\frac{5π}{6}$,π].…(12分)
点评 本题考查了平面向量的应用问题,也考查了三角函数的图象与性质的应用问题,是基础题目.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{2}}{9}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
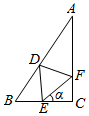 △ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.
△ABC中,已知:AB=2,BC=1,CA=$\sqrt{3}$,分别在边AB,BC,CA上取点D,E,F,使△DEF是等边三角形(如图),设∠FEC=α,问当sinα=$\frac{2\sqrt{7}}{7}$时,△DEF的边长最短.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
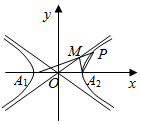 设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )
设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的顶点为A1,A2,P为双曲线上一点,直线PA1交双曲线C的一条渐近线于M点,直线A2M和A2P的斜率分别为k1,k2,若A2M⊥PA1且k1+4k2=0,则双曲线C离心率为( )| A. | 2 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{6}}{12}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{6}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}+1$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com