
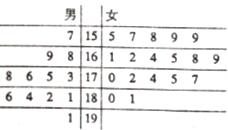
 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):分析 (I)利用茎叶图能求出男生跳远成绩的中位数.
(Ⅱ)用分层抽样的方法,求出每个运动员被抽中的概率,根据茎叶图,女生有18人,由此能求出抽取的女生的人数.
(Ⅲ)依题意,男生、女生测试成绩合格的分别有8人、10人,X的取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(I)利用茎叶图,得男生跳远成绩的中位数$\frac{176+178}{2}=177$(cm).…(2分)
(Ⅱ)用分层抽样的方法,每个运动员被抽中的概率是$\frac{5}{30}=\frac{1}{6}$,…(4分)
根据茎叶图,女生有18人,
∴抽取的女生有$18×\frac{1}{6}=3$(人);…(6分)
(Ⅲ)依题意,男生、女生测试成绩合格的分别有8人、10人…(7分)
X的取值为0,1,2,
则$P(X=0)=\frac{{C_{10}^2}}{{C_{18}^2}}=\frac{5}{17}$,
$P(X=1)=\frac{{C_8^1C_{10}^1}}{{C_{18}^2}}=\frac{80}{153}$,
$P(X=2)=\frac{C_8^2}{{C_{18}^2}}=\frac{28}{153}$,…(10分)
X的分布列如下:
| X | 0 | 1 | 2 |
| P | $\frac{5}{17}$ | $\frac{80}{153}$ | $\frac{28}{153}$ |
点评 本题考查茎叶图、分层抽样的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.
如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
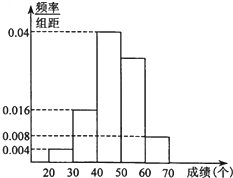 体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.
体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com