
分析 (1)利用导数的几何意义求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)分类讨论,利用函数的单调性,即可求实数t的最大值.
解答 解:(1)由题意x∈(0,+∞)且f′(x)=$\frac{x+1-xlnx}{{x(x+1)}^{2}}$,
∴f′(1)=$\frac{2-0}{4}$=$\frac{1}{2}$,又f(1)=$\frac{0}{2}$=0,
∴f(x)在点(1,f(1))处的切线方程为y-0=$\frac{1}{2}$(x-1),
即x-2y-1=0.
(2)由题意知 $\frac{lnx}{x+1}$-$\frac{lnx}{x-1}$-$\frac{t}{x}$>0,
设g(x)=$\frac{lnx}{x+1}$-$\frac{lnx}{x-1}$-$\frac{t}{x}$,
则g′(x)=$\frac{1}{1{-x}^{2}}$[2lnx+$\frac{t{(x}^{2}-1)}{x}$],
设h(x)=2lnx+$\frac{t{(x}^{2}-1)}{x}$,
则h′(x)=$\frac{2}{x}$+t(1+$\frac{1}{{x}^{2}}$)=$\frac{{tx}^{2}+2x+t}{{x}^{2}}$,
当t≥0时,∵x>0,∴h'(x)>0,∴h(x)在(0,+∞)上单调递增,
又h(1)=0,∴x∈(0,1)时,h(x)<0,
又 $\frac{1}{1{-x}^{2}}$>0,∴g(x)<0不符合题意.
当t<0时,设ϕ(x)=tx2+2x+t,
①若△=4-4t2≤0即t≤1时,ϕ(x)≤0恒成立,即h'(x)≤0在(0,+∞)恒成立,
∴h(x)在(0,+∞)上单调递减,
又h(1)=0,∴x∈(0,1)时,h(x)>0,$\frac{1}{1{-x}^{2}}$>0,g(x)>0,
x∈(1,+∞)时,h(x)<0,$\frac{1}{1{-x}^{2}}$<0,g(x)>0,符合题意.
②若△=4-4t2>0即-1<t<0时,ϕ(x)的对称轴x=-$\frac{1}{t}$>1,
∴ϕ(x)在(1,-$\frac{1}{t}$)上单调递增,
∴x∈(1,-$\frac{1}{t}$)时,ϕ(x)>ϕ(1)=2+2t>0,∴h'(x)>0,
∴h(x)在(1,-$\frac{1}{t}$)上单调递增,
∴h(x)>h(1)=0,而 $\frac{1}{1{-x}^{2}}$<0,
∴g(x)<0,不符合题意.
综上所述t≤-1,
∴t的最大值为-1.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查不等式的证明,体现分类讨论的数学思想,属于中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
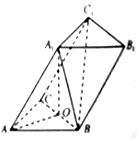 如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
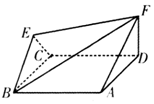 如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD,$FD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com