
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AE},\overrightarrow{AC}$,根据平面向量的基本定理列出方程解出m,n.
解答 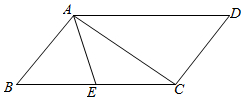 解:∵四边形ABCD是平行四边形,∴$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.
解:∵四边形ABCD是平行四边形,∴$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.
∵E是BC的中点,∴$\overrightarrow{AE}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$,
∴$\overrightarrow{AC}$=m$\overrightarrow{AE}$+n$\overrightarrow{AD}$=m$\overrightarrow{AB}$+$\frac{m}{2}\overrightarrow{AD}$+n$\overrightarrow{AD}$=m$\overrightarrow{AB}$+($\frac{m}{2}+n$)$\overrightarrow{AD}$.
∴$\left\{\begin{array}{l}{m=1}\\{\frac{m}{2}+n=1}\end{array}\right.$,解得m=1,n=$\frac{1}{2}$.∴m+n=$\frac{3}{2}$.
故选:C.
点评 本题考查了平面向量的基本定理,属于基础题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
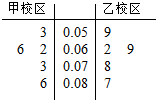 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )| A. | 甲校区较小 | B. | 乙校区较小 | ||
| C. | 甲乙两个校区相等 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{8}{x}$ | B. | $\frac{8}{x}$ | C. | -$\frac{4}{x}$ | D. | $\frac{4}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 165 | 160 | 175 | 155 | 170 |
| y | 58 | 52 | 62 | 43 | 60 |
| A. | -96.8 | B. | 96.8 | C. | -104.4 | D. | 104.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{2}}{6}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com