
分析 由正弦函数的图象特点,分别计算每一个最大值时对应的位置,确定第50个最值的取值范围解不等式即可.
解答 解:由正弦函数的图象特点,函数出现有50个最大值至少出现49$\frac{1}{4}$个周期
由题意数f(x)=2sin(ωx+$\frac{π}{3}$)(ω>0)在区间[0,20]上至少有50个最大值
则49$\frac{1}{4}$T≤20⇒$\frac{197}{4}•\frac{2π}{ω}$≤20,
可得ω≥$\frac{197π}{40}$
故答案为:ω≥$\frac{197π}{40}$,
第一个最大值的位置为ωx+$\frac{π}{3}$=$\frac{π}{2}$,
第2个最大值的位置为ωx+$\frac{π}{3}$=$\frac{π}{2}$+2π,
第3个最大值的位置为ωx+$\frac{π}{3}$=$\frac{π}{2}$+2×2π,
…
第50个最大值的位置为ωx+$\frac{π}{3}$=$\frac{π}{2}$+49×2π,
第51个最大值的位置为ωx+$\frac{π}{3}$=$\frac{π}{2}$+50×2π,
则$\frac{π}{2}$+49×2π≤20ω+$\frac{π}{3}$<$\frac{π}{2}$+50×2π,
解得$\frac{π}{120}$+$\frac{49π}{10}$≤ω<$\frac{π}{120}$+50π,
故答案为:[$\frac{π}{120}$+$\frac{49π}{10}$,$\frac{π}{120}$+50π)
点评 本题主要考查了正弦函数的性质.根据条件分别确定每一个最值对应的横坐标,确定第50个最值的取值范围是解决本题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
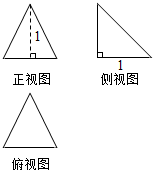
| A. | $\frac{{\sqrt{3}+\sqrt{7}+4}}{4}$ | B. | $\frac{{\sqrt{6}+2}}{2}$ | C. | $\frac{{\sqrt{2}+\sqrt{7}+1}}{2}$ | D. | $\frac{{\sqrt{2}+\sqrt{5}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A?B | B. | A=B | C. | A∩B=B | D. | A∪B=(0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com