
分析 (1)设直线方程为x-2y+c=0,代入(3,0),可得c,即可求出直线方程;
(2)先根据两条直线的夹角公式求出直线的斜率,用点斜式写出直线的方程,最后结果化为一般式.
解答 解:(1)设直线方程为x-2y+c=0,
代入(3,0),可得c=-3,
∴直线方程为x-2y-3=0;
(2)设所求直线的斜率为k,由题意得tan45°=|$\frac{-\frac{5}{2}-k}{1-\frac{5}{2}k}$|=1,
解得k1=$\frac{7}{3}$,k2=-$\frac{3}{7}$,
∵直线l′经过点P(2,1)
∴直线的方程为7x-3y-11=0和3x+7y-13=0
点评 本题考查两条直线的夹角公式的应用,以及用点斜式求直线的方程,本题解题的关键是根据夹角公式做出要求直线的斜率,本题是一个基础题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
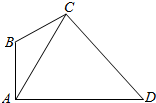 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
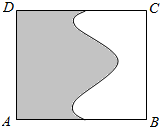 如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.
如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
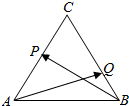 如图,在△ABC中,已知$\overrightarrow{AP}$=$\overrightarrow{PC}$,$\overrightarrow{CQ}$=2$\overrightarrow{QB}$,设$\overrightarrow{BP}$=m•$\overrightarrow{AB}$+n•$\overrightarrow{AC}$.
如图,在△ABC中,已知$\overrightarrow{AP}$=$\overrightarrow{PC}$,$\overrightarrow{CQ}$=2$\overrightarrow{QB}$,设$\overrightarrow{BP}$=m•$\overrightarrow{AB}$+n•$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com