
一学生参加市场营销调查活动,从某商场得到11月份新款家电M的部分销售资料.资料显示:11月2日开始,每天的销售量比前一天多t台(t为常数),期间某天由于商家提高了家电M的价格,从当天起,每天的销售量比前一天少2台.11月份前2天共售出8台,11月5日的销售量为18台.
(1)若商家在11月1日至15日之间未提价,试求这15天家电M的总销售量.
(2)若11月1日至15日的总销售量为414台,试求11月份的哪一天,该商场售出家电M的台数最多?并求这一天售出的台数.
解:(1)依题意得,11月1日至11月15日该商场家电M每天的销售量组成公差为t的等差数列{an},由已知得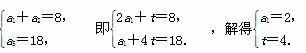
所以这15天的总销售量为S15=15×2+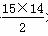 ×4=450(台).
×4=450(台).
(2)设从11月1日起,第n天销售量最多,1≤n≤30,n∈N*,
由(1)知,在11月1日至15日之间未提价,则这15天家电M的总销售量为450台,已知11月1日至15日的总销售量为414台,414<450.所以n<15.
若n=5,则S15=5×2+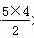 ×4+10×16+
×4+10×16+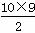 ×(-2)=120<414,由此可得n>5.
×(-2)=120<414,由此可得n>5.
从而前n天每天的销售量组成一个首项为2,公差为4的等差数列,第n+1天开始每天的销售量组成首项为4n-4,公差为-2的等差数列.
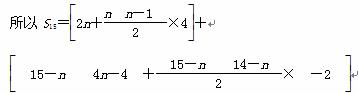 =2n2-5n2+93n-270=-3n2+93n-270,
=2n2-5n2+93n-270=-3n2+93n-270,
由已知得S15=414,即-3n2+93n-270=414,
即n2-31n+228=0;
解得n=12或n=19(舍去).
∴n=12,2+11×4=46.
故11月12日,该商场售出家电M的台数最多,这一天售出的台数为46.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知向量a=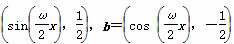 (ω>0,x≥0),函数f(x)=a·b的第n(n∈N*)个零点记作xn(从左向右依次计数),则所有xn组成数列{xn}.
(ω>0,x≥0),函数f(x)=a·b的第n(n∈N*)个零点记作xn(从左向右依次计数),则所有xn组成数列{xn}.
(1)若ω=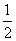 ,求x2;
,求x2;
(2)若函数f(x)的最小正周期为π,求数列{xn}的前100项和S100.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x+tan x,项数为17的等差数列{an}满足an∈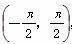 ,且公差d≠0.若f(a1)+f(a2)+…+f(a17)=0,则当k=________时,f(ak)=0.
,且公差d≠0.若f(a1)+f(a2)+…+f(a17)=0,则当k=________时,f(ak)=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
经过点P(1,4)的直线在两坐标轴上的截距都是正的,且截距之和最小,则直线的方程为( )
A.x+2y-6=0 B.2x+y-6=0
C.x-2y+7=0 D.x-2y-7=0
查看答案和解析>>
科目:高中数学 来源: 题型:
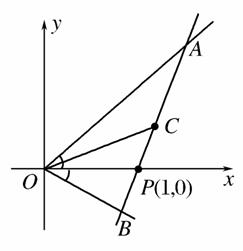
如图,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y= x上时,求直线AB的方程.
x上时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
设F1、F2分别是椭圆E: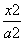 +
+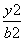 =1(a>b>0)的左、右焦点,M、N分别为其短轴的两个端点,且四边形MF1NF2的周长为4,设过F1的直线l与E相交于A、B两点,且|AB|=
=1(a>b>0)的左、右焦点,M、N分别为其短轴的两个端点,且四边形MF1NF2的周长为4,设过F1的直线l与E相交于A、B两点,且|AB|=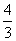 .
.
(1)求|AF2|·|BF2|的最大值;
(2)若直线l的倾斜角为45°,求△ABF2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com