
设F1、F2分别是椭圆E: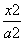 +
+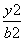 =1(a>b>0)的左、右焦点,M、N分别为其短轴的两个端点,且四边形MF1NF2的周长为4,设过F1的直线l与E相交于A、B两点,且|AB|=
=1(a>b>0)的左、右焦点,M、N分别为其短轴的两个端点,且四边形MF1NF2的周长为4,设过F1的直线l与E相交于A、B两点,且|AB|=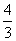 .
.
(1)求|AF2|·|BF2|的最大值;
(2)若直线l的倾斜角为45°,求△ABF2的面积.
解:(1)因为四边形MF1NF2为菱形,又其周长为4,故a=1
由椭圆定义知|AF2|+|AB|+|BF2|=4a=4,又因为|AB|=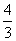 ,
,
所以|AF2|+|BF2|= ,
,
所以|AF2|·|BF2|≤ =
=
当且仅当|AF2|=|BF2|=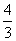 时,等号成立.
时,等号成立.
(此时AB⊥x轴,故可得A点坐标为 ,代入椭圆E的方程x2+
,代入椭圆E的方程x2+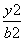 =1得b=
=1得b= <1,即当且仅当b=
<1,即当且仅当b= 时,|AF2|=|BF2|=
时,|AF2|=|BF2|=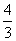 )
)
所以|AF2|·|BF2|的最大值为 .
.
(2)因为直线l的倾斜角为45°,所以可设l的方程为y=x+c,其中c= 

由(1)知椭圆E的方程为x2+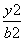 =1
=1
所以,设A(x1,y1),B(x2,y2),则A、B两点坐标满足方程组
化简得(1+b2)x2+2cx+1-2b2=0
则x1+x2= ,x1x2=
,x1x2=
因为直线l的斜率为1,所以|AB|= |x1-x2|
|x1-x2|
即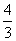 =
= |x1-x2|,所以
|x1-x2|,所以 =(x1+x2)2-4x1x2
=(x1+x2)2-4x1x2
 =
= ,得b2=
,得b2= ,b=
,b=
所以c= ,l的方程为:y=x+
,l的方程为:y=x+
F2到l的距离d=1.
所以S△ABC= |AB|×1=
|AB|×1= ×
×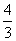 ×1=
×1= .
.


科目:高中数学 来源: 题型:
一学生参加市场营销调查活动,从某商场得到11月份新款家电M的部分销售资料.资料显示:11月2日开始,每天的销售量比前一天多t台(t为常数),期间某天由于商家提高了家电M的价格,从当天起,每天的销售量比前一天少2台.11月份前2天共售出8台,11月5日的销售量为18台.
(1)若商家在11月1日至15日之间未提价,试求这15天家电M的总销售量.
(2)若11月1日至15日的总销售量为414台,试求11月份的哪一天,该商场售出家电M的台数最多?并求这一天售出的台数.
查看答案和解析>>
科目:高中数学 来源: 题型:
如右图所示,圆O1和圆O2的半径长都等于1,|O1O2|=4.过动点P分别作圆O1,圆O2的切线PM,PN(M,N为切点),使得|PM|= |PN|.试建立平面直角坐标系,并求动点P的轨迹方程.
|PN|.试建立平面直角坐标系,并求动点P的轨迹方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
设m,n∈R,若直线l:mx+ny-1=0与x轴交于点A,与y轴交于点B,且l与圆x2+y2=4相交所得弦长为2,O为坐标原点,则△OAB面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
圆锥曲线C的两个焦点分别为F1,F2,若曲线C上存在点P满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线C的离心率为( )
A.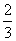 或
或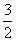 B.
B.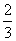 或2
或2
C.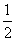 或2 D.
或2 D.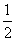 或
或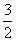
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F1,F2分别是双曲线x2-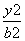 =1的左、右焦点,A是双曲线上在第一象限内的点,若|AF2|=2且∠F1AF2=45°.延长AF2交双曲线右支于点B,则△F1AB的面积等于________.
=1的左、右焦点,A是双曲线上在第一象限内的点,若|AF2|=2且∠F1AF2=45°.延长AF2交双曲线右支于点B,则△F1AB的面积等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l1:4x-3y+6=0和直线l2:x=-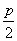 ;若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
;若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
(1)求抛物线C的方程;
(2)若以拋物线上任意一点M为切点的直线l与直线l2交于点N,试问在x轴上是否存在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com