练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若点(m，n)在直线4x＋3y－10＝0上，则m2＋n2的最小值是(　　)

    A．2                                    B．2 

    C．4                                    D．2


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知公差不为0的等差数列{an}的首项为2，且a1，a2，a4成等比数列．

    (1)求数列{an}的通项公式；

    (2)令bn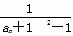＝ (n∈N*)，求数列{bn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一学生参加市场营销调查活动，从某商场得到11月份新款家电M的部分销售资料．资料显示：11月2日开始，每天的销售量比前一天多t台(t为常数)，期间某天由于商家提高了家电M的价格，从当天起，每天的销售量比前一天少2台.11月份前2天共售出8台，11月5日的销售量为18台．

    (1)若商家在11月1日至15日之间未提价，试求这15天家电M的总销售量．

    (2)若11月1日至15日的总销售量为414台，试求11月份的哪一天，该商场售出家电M的台数最多？并求这一天售出的台数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a∈R，则“a＝1”是“直线l1：ax＋2y－1＝0与直线l2：x＋(a＋1)y＋4＝0平行”的(　　)

    A．充分不必要条件                       B．必要不充分条件

    C．充分必要条件                         D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面直角坐标系中，过原点O的直线l与曲线y＝ex－1交于不同的A，B两点，分别过点A，B作y轴的平行线，与曲线y＝ln x交于点C，D，则直线CD的斜率是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点M是直线3x＋4y－2＝0上的动点，点N为圆(x＋1)2＋(y＋1)2＝1上的动点，则|MN|的最小值是(　　)

    A.                                    B．1 

    C.                                    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如右图所示，圆O1和圆O2的半径长都等于1，|O1O2|＝4.过动点P分别作圆O1，圆O2的切线PM，PN(M，N为切点)，使得|PM|＝|PN|.试建立平面直角坐标系，并求动点P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设m，n∈R，若直线l：mx＋ny－1＝0与x轴交于点A，与y轴交于点B，且l与圆x2＋y2＝4相交所得弦长为2，O为坐标原点，则△OAB面积的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l1：4x－3y＋6＝0和直线l2：x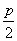＝－；若拋物线C：y2＝2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.

    (1)求抛物线C的方程；

    (2)若以拋物线上任意一点M为切点的直线l与直线l2交于点N，试问在x轴上是否存在定点Q，使Q点在以MN为直径的圆上，若存在，求出点Q的坐标，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案