考点：二项式系数的性质
专题：二项式定理
分析：在（2-
x）
100=a
0+a
1x+a
2x
2+…a
100x
100中，
（1）令x=0可得a
0 的值；
（2）令x=1，可得a
0+a
1+a
2+a
3+…+a
100 =
(2-)100 ①，从而求得a
1+a
2+a
3+…+a
100 的值；
（3）令x=-1，可得2
100-a
1+a
2-a
3+…+a
100 =
(2+)100 ②，由①②求得a
1+a
3+a
5…+a
99 的值，
（4）由①②可得a
1+a
3+a
5…+a
99 的值、以及a
0+a
2+…+a
100 的值，从而求得（a
0+a
2+…+a
100）
2-（a
1+a
3+…+a
99）
2的值．
（5）|a
0|+|a
1|+…+|a
100|，即（2+
x）
100的展开式中各项系数的和，在（2+
x）
100的展开式中，令x=1，可得结果．
解答：
解：在（2-
x）
100=a
0+a
1x+a
2x
2+…a
100x
100中，
（1）令x=0可得a
0=2
100．
（2）令x=1，可得2
100+a
1+a
2+a
3+…+a
100 =
(2-)100 ①，∴a
1+a
2+a
3+…+a
100 =
(2-)100-2
100．
（3）令x=-1，可得得2
100-a
1+a
2-a
3+…+a
100 =
(2+)100 ②，
由①②求得a
1+a
3+a
5…+a
99 =
．
（4）由①②还可得到 a
0+a
2+…+a
100 =
，
∴（a
0+a
2+…+a
100）
2-（a
1+a
3+…+a
99）
2 =（a
0+a
1+a
2+…a
100）（a
0-a
1+a
2+…+a
100）=（2-
）
100 •（2+
）
100 =1．
（5）|a
0|+|a
1|+…+|a
100|即（2+
x）
100的展开式中各项系数的和，
在（2+
x）
100的展开式中，令x=1，可得各项系数的和为
(2+)100．
点评：本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于基础题．
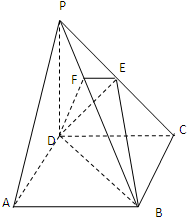如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F，求证：PF=