
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 边上的高,沿
边上的高,沿![]() 把
把![]() 折起,使
折起,使![]() 。
。

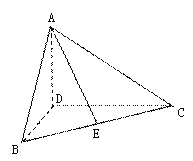
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)![]() 为
为![]() 的中点,求
的中点,求![]() 与底面
与底面![]() 所成角的正切值。
所成角的正切值。
【答案】(1)见解析;(2)![]() .
.
【解析】此题主要考查面面垂直和异面直线夹角公式的求法,第二问解题的关键是作出辅助线,此题是一道中档题,也是高考必考题;(1)已知在△ABC中,AD是BC上的高,沿AD把△ABC折起,使∠BDC=60°,可得AD⊥DC,AD⊥DB,根据面面垂直的判定定理进行求解;
(2)作辅助线,取DC中点F,连接EF,则EF∥BD,可得∠AEF为异面直线AE与BD所成的角,再根据余弦定理和向量公式进行求解;
解(Ⅰ)∵折起前AD是BC边上的高,
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,又DB![]() DC=D,
DC=D,
∴AD⊥平面BDC,∵AD 平面![]() 平面BDC.
平面BDC. ![]() 平面ABD
平面ABD![]() 平面BDC。----4分
平面BDC。----4分
(Ⅱ)由∠ BDC=![]() 及(Ⅰ)知DA,DB,DC两两垂直,不防设
及(Ⅰ)知DA,DB,DC两两垂直,不防设![]() =1,以D为坐标原点,以
=1,以D为坐标原点,以![]() 所在直线
所在直线![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,

易得D(0,0,0),B(1,0,0),C(0,3,0),A(0,0, ![]() ),E(
),E(![]() ,
, ![]() ,0),
,0),
![]() =
=![]() ,
, ![]() =(1,0,0,),
=(1,0,0,),
![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为
![]() <
<![]() ,
, ![]() >=
>=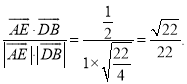
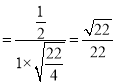 .--------12分
.--------12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .当
.当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(1)以![]() 为直径的圆能否经过点
为直径的圆能否经过点![]() ?说明理由;
?说明理由;
(2)过![]() ,
, ![]() ,
, ![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市地产数据研究所的数据显示,2016年该市新建住宅销售均价走势如下图所示,3月至7月房价上涨过快,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
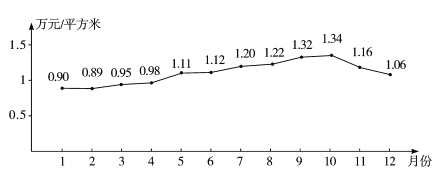
(1)地产数据研究所发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试求
之间具有较强的线性相关关系,试求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)政府若不调控,依次相关关系预测第12月份该市新建住宅的销售均价.
参考数据: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公示分别为:
中斜率和截距的最小二乘法估计公示分别为:
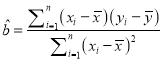 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)满足f(2)=0,且在(﹣∞,0)上是增函数;又定义行列式![]() =a1a4﹣a2a3; 函数g(θ)=
=a1a4﹣a2a3; 函数g(θ)=![]() (其中0≤θ≤
(其中0≤θ≤![]() ).
).
(1)证明:函数f(x)在(0,+∞)上也是增函数;
(2)若函数g(θ)的最大值为4,求m的值;
(3)若记集合M={m|任意的0≤θ≤![]() , g(θ)>0},N={m|任意的0≤θ≤
, g(θ)>0},N={m|任意的0≤θ≤![]() , f[g(θ)]<0},求M∩N.
, f[g(θ)]<0},求M∩N.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,点P到两点(0,﹣![]() ),(0,
),(0,![]() )的距离之和等于4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
)的距离之和等于4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
(1)写出C的方程;
(2)若![]() ⊥
⊥![]() , 求k的值.
, 求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn,且![]() ,令cn=b2n(n∈N*),求数列{cn}的前n项和Rn.
,令cn=b2n(n∈N*),求数列{cn}的前n项和Rn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com