
【题目】已知定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)满足f(2)=0,且在(﹣∞,0)上是增函数;又定义行列式![]() =a1a4﹣a2a3; 函数g(θ)=
=a1a4﹣a2a3; 函数g(θ)=![]() (其中0≤θ≤
(其中0≤θ≤![]() ).
).
(1)证明:函数f(x)在(0,+∞)上也是增函数;
(2)若函数g(θ)的最大值为4,求m的值;
(3)若记集合M={m|任意的0≤θ≤![]() , g(θ)>0},N={m|任意的0≤θ≤
, g(θ)>0},N={m|任意的0≤θ≤![]() , f[g(θ)]<0},求M∩N.
, f[g(θ)]<0},求M∩N.
【答案】证明:(1)在(0,+∞)上任取x1 , x2 , 令x1<x2 ,
∵定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)满足f(2)=0,且在(﹣∞,0)上是增函数,
∴f(x1)﹣f(x2)=﹣f(﹣x1)+f(﹣x2)=f(﹣x2)﹣f(﹣x1)<0,
∴函数f(x)在(0,+∞)上也是增函数.
解:(2)g(θ)=![]()
=sin2θ+mcosθ﹣3m
=1﹣cos2θ+mcosθ﹣3m,
=﹣(cosθ﹣![]() )2+
)2+![]() ,
,
∵函数g(θ)的最大值为4,f(x)在(﹣∞,0)上是增函数,又f(x)是奇函数,
∴f(x)在(0,+∞)也是增函数,
∵θ∈[0,![]() ],∴cosθ∈[0,1],
],∴cosθ∈[0,1],
g(θ)的最大值只可能在cosθ=0(![]()
![]() ),cosθ=1(
),cosθ=1(![]()
![]() ),cosθ=
),cosθ=![]() (0<
(0<![]()
![]() )处取得,
)处取得,
若cosθ=0,g(θ)=4,则有1﹣3m=4,m=﹣1,此时![]() =-
=-![]() ,符合;
,符合;
若cosθ=1,g(θ)=4,则有﹣2m=4,m=﹣2,此时![]() =-1,不符合;
=-1,不符合;
若cosθ=![]() ,g(θ)=4,则有
,g(θ)=4,则有![]() =4,m=6+4
=4,m=6+4![]() 或m=6﹣4
或m=6﹣4![]() ,此时
,此时![]() =3+2
=3+2![]() 或m=3﹣2
或m=3﹣2![]() ,不符合;
,不符合;
综上,m=﹣1.
(3)∵f(x)是定义在(﹣∞,0)∪(0,+∞)上的奇函数,且满足f(2)=0,∴f(﹣2)=0,
又f(x)在(﹣∞,0),(0,+∞)上均是增函数,
由f[g(θ)]<0,得g(θ)<﹣2,或2>g(θ)>0,
又M={m|恒有g(θ)>0},N={m|恒有f[g(θ)]<0}={m|恒有g(θ)<﹣2,或2>g(θ)>0},
∴M∩N={m|恒有0<g(θ)<2},即不等式0<﹣cos2θ+mcosθ﹣3m+1<2在θ∈[0,![]() ]恒成立,
]恒成立,
当m>![]() =
=![]()
=﹣(3﹣cosθ)﹣(![]() )+6=﹣[(3﹣cosθ)+(
)+6=﹣[(3﹣cosθ)+(![]() )]+6,
)]+6,
∵θ∈[0,![]() ],∴cosθ∈[0,1],3﹣cosθ∈[2,3],
],∴cosθ∈[0,1],3﹣cosθ∈[2,3],
∴7≥(3﹣cosθ)+(![]() )
)![]() ,﹣[(3﹣cosθ)+(
,﹣[(3﹣cosθ)+(![]() )]+6∈[﹣1,﹣
)]+6∈[﹣1,﹣![]() ],
],
此时,m>﹣![]() ;
;![]() =﹣(3﹣cosθ)﹣(
=﹣(3﹣cosθ)﹣(![]() )+6=﹣[(3﹣cosθ)+(
)+6=﹣[(3﹣cosθ)+(![]() )]+6,
)]+6,
∵θ∈[0,![]() ],∴cosθ∈[0,1],3﹣cosθ∈[2,3],
],∴cosθ∈[0,1],3﹣cosθ∈[2,3],
∴7≥(3﹣cosθ)+(![]() )
)![]() ,﹣[(3﹣cosθ)+(
,﹣[(3﹣cosθ)+(![]() )]+6∈[﹣1,﹣
)]+6∈[﹣1,﹣![]() ],
],
此时,m>﹣![]() .
.
当m<![]() =
=![]()
=﹣(3﹣cosθ)﹣(![]() )+6
)+6
=﹣[(3﹣cosθ)+(![]() )]+6,
)]+6,
∴6≥(3﹣cosθ)+(![]() )
)![]() ,﹣[(3﹣cosθ)+(
,﹣[(3﹣cosθ)+(![]() )]+6∈[0,6﹣4
)]+6∈[0,6﹣4![]() ],
],
此时,m<0;
综上,m∈(﹣![]() ,0).
,0).
∴M∩N=(﹣![]() ,0).
,0).
【解析】(1)利用定义法能证明函数f(x)在(0,+∞)上也是增函数.
(2)由已知可判断f(x)在(0,+∞)上的单调性,由定义表示出g(θ),根据二次函数的性质分类讨论可表示出其最大值,令其为4可求m值;
(3)由f[g(θ)]<0,得g(θ)<﹣2,或2>g(θ)>0,则M={m|恒有g(θ)>0},N={m|恒有f[g(θ)]<0}={m|恒有g(θ)<﹣2,或2>g(θ)>0},从而M∩N={m|恒有0<g(θ)<2},转化为不等式0<﹣cos2θ+mcosθ﹣3m+1<2在θ∈[0,![]() ]恒成立,分离出参数m后,转化为求函数的最值即可,变形后借助“对勾函数”的性质可求得最值;
]恒成立,分离出参数m后,转化为求函数的最值即可,变形后借助“对勾函数”的性质可求得最值;


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:
【题目】某工厂拟造一座平面为长方形,面积为![]() 的三级污水处理池.由于地形限制,长、宽都不能超过
的三级污水处理池.由于地形限制,长、宽都不能超过![]() ,处理池的高度一定.如果池的四周墙壁的造价为
,处理池的高度一定.如果池的四周墙壁的造价为![]() 元
元![]() ,中间两道隔墙的造价为
,中间两道隔墙的造价为![]() 元
元![]() ,池底的造价为
,池底的造价为![]() 元
元![]() ,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
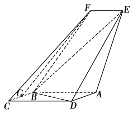
(1)求证:FG![]() 平面BED;
平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 在
在![]() 和
和![]() 处取得极值,且
处取得极值,且![]() ,曲线
,曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)证明关于![]() 的方程
的方程![]() 至多只有两个实数根(其中
至多只有两个实数根(其中![]() 是
是![]() 的导函数,
的导函数, ![]() 是自然对数的底数).
是自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x﹣2x+1+3,当x∈[﹣2,1]时,f(x)的最大值为m,最小值为n,
(1)若角α的终边经过点P(m,n),求sinα+cosα的值;
(2)g(x)=mcos(nx+![]() )+n,求g(x)的最大值及自变量x的取值集合.
)+n,求g(x)的最大值及自变量x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过
,过![]() 上一点
上一点![]() 的切线
的切线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 且斜率不为
且斜率不为![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,试问
两点,试问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得 ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.
的左顶点为A,右焦点为F,过点F的直线交椭圆于B,C两点.
(1)求该椭圆的离心率;
(2)设直线AB和AC分别与直线x=4交于点M,N,问:x轴上是否存在定点P使得MP⊥NP?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com