
分析 将x=c代入双曲线方程求出点M的坐标,通过解直角三角形列出三参数a,b,c的关系,求出离心率的值.
解答 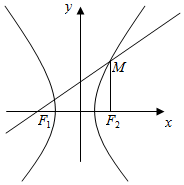 解:将x=c代入双曲线的方程$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)得y=$\frac{{b}^{2}}{a}$,
解:将x=c代入双曲线的方程$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)得y=$\frac{{b}^{2}}{a}$,
即M(c,$\frac{{b}^{2}}{a}$).
在△MF1F2中tan45°=$\frac{\frac{{b}^{2}}{a}}{2c}$=1
即$\frac{{c}^{2}-{a}^{2}}{2ac}=1$,解得e=$\frac{c}{a}$=$\sqrt{2}$+1.
故答案为:$\sqrt{2}$+1
点评 本题考查双曲线离心率的计算,根据双曲线中三参数的关系:c2=a2+b2,建立方程关系是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
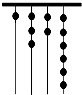 远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,如图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满七进一,根据图示可知,孩子已经出生的天数是( )
远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,如图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满七进一,根据图示可知,孩子已经出生的天数是( )| A. | 336 | B. | 510 | C. | 1326 | D. | 3603 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.4万元 | B. | 11.8万元 | C. | 12.0万元 | D. | 12.2万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | m | 5.6 | 6.1 | 7.4 | 9.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房屋大小 x/m2 | 80 | 105 | 110 | 115 | 135 |
| 销售价格y/万元 | 18.4 | 22 | 21.6 | 24.8 | 29.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com