
分析 设点P的坐标为(x,y),点Q的坐标为(x0,y0),由三角形内角平分线定理写出方程组,解出x0和y0,代入已知圆的方程即可.
解答 解:在△AOQ中,
∵OP是∠AOQ的平分线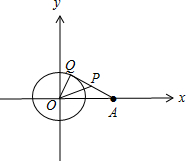
∴$\frac{|AP|}{|QP|}=\frac{|OA|}{|OQ|}=2$,
设P点坐标为(x,y);Q点坐标为(x0,y0),
∴$\left\{\begin{array}{l}{x=\frac{2+2{x}_{0}}{1+2}}\\{y=\frac{0+2{y}_{0}}{1+2}}\end{array}\right.$,得$\left\{\begin{array}{l}{{x}_{0}=\frac{3x-2}{2}}\\{{y}_{0}=\frac{3}{2}y}\end{array}\right.$,
∵Q(x0,y0)在圆x2+y2=1上运动,
∴x02+y02=1
即$(\frac{3x-2}{2})^{2}+(\frac{3}{2}y)^{2}=1$,
∴$(x-\frac{2}{3})^{2}+{y}^{2}=\frac{4}{9}$.
∴动点P的轨迹为$(x-\frac{2}{3})^{2}+{y}^{2}=\frac{4}{9}$.
点评 本题考查轨迹方程的求法,训练了代入法求曲线的轨迹方程,运用此法注意将要求的动点坐标设为(x,y),最后求得的x与y的关系式即为所求,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,1) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | (0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | 3 | C. | $\sqrt{15}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com