
分析 由直线方程求出直线的倾斜角,再分别写出终边落在直线向上和向下方向上的角的集合,由集合的并集运算求出终边落在直线y=$\sqrt{3}$x上的角的集合.
解答 解:∵直线y=$\sqrt{3}$x的斜率为,则倾斜角为60°,
∴终边落在射线y=$\sqrt{3}$x(x≥0)上的角的集合是S1={α|α=60°+k•360°,k∈Z},
终边落在射线y=$\sqrt{3}$x(x≤0)上的角的集合是S2={α|α=240°+k•360°,k∈Z},
∴终边落在直线y=$\sqrt{3}$x上的角的集合是:
S={α|α=60°+k•360°,k∈Z}∪{α|α=240°+k•360°,k∈Z}
={α|α=60°+2k•180°,k∈Z}∪{α|α=60°+(2k+1)•180°,k∈Z}
={α|α=60°+n•180°,n∈Z}.
故答案为:{α|α=60°+n•180°,n∈Z}.
点评 本题考查了终边相同角的集合求法,以及集合的并集的运算,需要将集合的元素化为统一的形式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 10 | 15 | 20 | 25 | 30 |
| y | 1 003 | 1 005 | 1 010 | 1 011 | 1 014 |
| A. | $\widehat{y}$=0.56x+997.4 | B. | $\widehat{y}$=0.63x-231.2 | C. | $\widehat{y}$=0.56x+501.4 | D. | $\widehat{y}$=60.4x+400.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
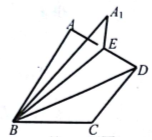 如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )| A. | BC与平面A1BE内某直线平行 | B. | CD∥平面A1BE | ||
| C. | BC与平面A1BE内某直线垂直 | D. | BC⊥A1B |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com