
 和房屋的面积
和房屋的面积 的数据:
的数据: 房屋面积 | 110 | 90 | 80 | 100 | 120 |
| 销售价格(万元) | 33 | 31 | 28 | 34 | 39 |
 时的销售价格.
时的销售价格. ,
,  ,
, ,
, )
) 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 。
。
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 必过
必过 ;
; 的零点有2个;
的零点有2个; 的图象与
的图象与 轴围成的图形面积是
轴围成的图形面积是 ;
; 是偶函数,且在区间
是偶函数,且在区间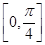 内单调递增;
内单调递增; 的最小正周期为
的最小正周期为 .其中真命题的序号是 。
.其中真命题的序号是 。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学(x分 | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.一组数据的平均数一定大于这组数据中的每个数据 |
| B.一组数据不可能有两个众数 |
| C.一组数据的中位数一定是这组数据中的某个数据 |
| D.一组数据的方差越大,说明这组数据的波动越大 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 名学生成绩进行统计时,把这
名学生成绩进行统计时,把这 名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有
名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有 名学生的物理成绩是自己的实际分数的概率是多少?
名学生的物理成绩是自己的实际分数的概率是多少? 表示数学成绩,用
表示数学成绩,用 表示物理成绩,求
表示物理成绩,求 与
与 的回归方程;
的回归方程; 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”. ,其中
,其中 ,
, ;
; ,残差和公式为:
,残差和公式为:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com