
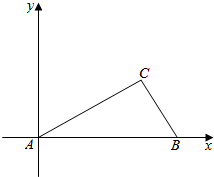
 如图,一边在x轴,一个顶点在原点△ABC的所有高都小于1,请问是否存在这样的B、C的位置,使得△ABC的面积大于2015?
如图,一边在x轴,一个顶点在原点△ABC的所有高都小于1,请问是否存在这样的B、C的位置,使得△ABC的面积大于2015? 分析 利用特殊点,找出B、C坐标,推出结果即可.
解答  解:存在这样的三角形,不妨取B(5000,0),如图:D(0,1),BD的方程为:y=$\frac{1}{5000}x-1$
解:存在这样的三角形,不妨取B(5000,0),如图:D(0,1),BD的方程为:y=$\frac{1}{5000}x-1$
取F(10100,1),可得AF的方程为:y=$\frac{1}{10100}x$
直线AF与直线DB的交点为:C,联立方程可得
C($\frac{505000}{51}$,$\frac{50}{51}$),此时三角形的三个顶点到三条边的距离都小于1,
并且三角形的面积为:$\frac{1}{2}×5000×\frac{50}{51}$≈2451>2015.
存在这样的三角形.
点评 本题考查三角形的判断,存在性问题的处理方法,考查计算能力.


科目:高中数学 来源: 题型:解答题
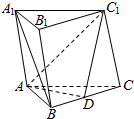 如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.
如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com