Question

19．已知函数 f （x）=$\left\{\begin{array}{l}{3^{-x}}-1，x＜0\\ 2\sqrt{x}，x≥0\end{array}\right.$，若函数 g （x）=f （x）-x-b 有三个零点，则实数b的取值范围为（　　）

• A． （0，1）
• B． （1，2）
• C． （1，2]
• D． （-∞，2]

Answer 1

分析 由题意可转化为函数f（x）与函数y=x+b的图象有且仅有3个交点，从而作图求解即可．

解答 解：若函数 g （x）=f （x）-x-b 有三个零点，
则f（x）和h（x）=x+b有3个交点，
画出函数f（x）和h（x）的图象，如图所示：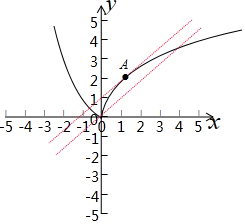
，
x＞0时，当h（x）=x+b和f（x）=2$\sqrt{x}$相切时，设切点A（x₀，y₀），
则f′（x₀）=$\frac{1}{\sqrt{{x}_{0}}}$=1，解得：x₀=1，故y₀=2，即A（1，2），
故此时，h（x）=x+1，直线和f（x）的图象有2个交点，结合图象，
0＜b＜1时满足题意，
故选：A．

点评 本题考查了导数的应用，函数图象的作法及函数的零点与函数的图象的交点的关系应用等，同时考查了数形结合的思想应用，属于中档题．