
分析 由a,b,c成等差数列,利用等差数列的性质得到2b=a+c,整理后与直线方程ax+by+c=0比较发现,直线ax+by+c=0恒过Q(1,-2),再由点P(-1,0)在动直线ax+by+c=0上的射影为M,得到PM与QM垂直,利用圆周角定理得到M在以PQ为直径的圆上,由P和Q的坐标,利用中点坐标公式求出圆心A的坐标,利用两点间的距离公式求出此圆的半径r,线段MN长度的最值即为M与圆心A的距离与半径的和与差,求出即可.
解答 解:∵a,b,c成等差数列,
∴2b=a+c,即a-2b+c=0,
可得方程ax+by+c=0恒过Q(1,-2),
又点P(-1,0)在动直线ax+by+c=0上的射影为M,
∴∠PMQ=90°,
∴M在以PQ为直径的圆上,
∴此圆的圆心A坐标为($\frac{1-1}{2}$,$\frac{-2+0}{2}$),即A(0,-1),半径r=$\frac{1}{2}$|PQ|=$\frac{1}{2}$$\sqrt{(1+1)^{2}+({-2)}^{2}}$=$\sqrt{2}$,
又N(3,3),
∴|AN|=5,
则|MN|max=5+$\sqrt{2}$,最小值为5-$\sqrt{2}$,所以线段MN的范围为:[5-$\sqrt{2}$,5+$\sqrt{2}$].
故答案为:[5-$\sqrt{2}$,5+$\sqrt{2}$].
点评 此题考查了等差数列的性质,恒过定点的直线方程,圆周角定理,线段中点坐标公式,以及两点间的距离公式,利用等差数列的性质得到2b=a+c,即a-2b+c=0是解本题的突破点.


科目:高中数学 来源: 题型:选择题
| A. | f(cosA)>f(sinB) | B. | f(sinA)>f(cosB) | C. | f(cosA)≥f(sinB) | D. | f(sinA)≥f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | B. | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ | C. | $\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AD}$ | D. | $\frac{2}{5}$$\overrightarrow{AB}$+$\frac{3}{5}$$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
设 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使得
,使得 ,则称
,则称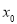 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (1,2] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com