在△ABC中.sinA:sinB:sinC=2:3:4.则cosC= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

在△ABC中，sinA：sinB：sinC=2：3：4，则cosC=

．

考点：余弦定理,正弦定理

专题：解三角形

分析：已知等式利用正弦定理化简得到三边之比，表示出三边长，利用余弦定理表示出cosC，将三边长代入即可求出cosC的值．

解答： 解：在△ABC中，sinA：sinB：sinC=2：3：4，
利用正弦定理化简得：a：b：c=2：3：4，
设a=2k，b=3k，c=4k，
∴cosC=

a2+b2-c2

2ab

4k2+9k2-16k2

12k2

．
故答案为：-

．

点评：此题考查了正弦、余弦定理，熟练掌握定理是解本题的关键．

练习册系列答案

正大图书中考试题汇编系列答案

名师面对面中考系列答案

小学英语一本通江苏凤凰教育出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

已知数列{a_n}的前n项和S_n满足S₁=-1，S_n+1+2S_n=-1（n∈N^*），数列{b_n}的通项公式为b_n=3n-4（n∈N^*）
（1）求数列{a_n}的通项公式；
（2）是否存在圆心在x轴上的圆C及互不相等的正整数n、m、k，使得三点A_n（b_n，a_n），A_m（b_m，a_m），A_k（b_k，a_k）落在圆C上？请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

定义在R上的奇函数f（x）在（0，+∞）上单调递减，且f（1）=0，则不等式xf（x）≥0的解集为

．

查看答案和解析>>

科目：高中数学 来源： 题型：

已知函数f（x）=

2x+3

，数列{a_n}满足a₁=1，a_n+1=f（

），n∈N^*．
（1）求数列{a_n}的通项公式；
（2）令b_n=

an-1an

（n≥2），b₁=3，S_n=b₁+b₂+…+b_n，若S_n＜

m-2004

对一切n∈N^*成立，求最小正整数m．

查看答案和解析>>

科目：高中数学 来源： 题型：

解方程：1.2^x=6．

查看答案和解析>>

科目：高中数学 来源： 题型：

如图所示，有一具开口向上的截面为抛物线型模具，上口AB宽2m，纵深OC为1.5m．
（l）当浇铸零件时，钢水面EF距AB 0.5m，求截面图中EF的宽度；
（2）现将此模具运往某地，考虑到运输中的各种因素，必须把它安置于一圆台型包装箱内，求使包装箱的体积最小时的圆台的上、下底面的半径．
V_圆台=

πh（r₁²+r₂²+r₁r₂），r₁，r₂为上、下底面的半径，h为高，参考数据

4	3

≈

．

查看答案和解析>>

科目：高中数学 来源： 题型：

请你设计一个LED霓虹灯灯箱．现有一批LED霓虹灯灯箱材料如图所示，ABCD是边长为60cm的正方形LED散片，边CD上有一以其中点M为圆心，半径为2cm的半圆形缺损，因此切去阴影部分（含半圆形缺损）所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于空间一点P，正好形成一个正四棱柱形状有盖的LED
霓虹灯灯箱，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xcm．
（1）用规格长×宽×高=145cm×145cm×75cm外包装盒来装你所设计的LED霓虹灯灯箱，灯箱彼此间隔空隙至多0.5cm，请问包装盒至少能装多少只LED霓虹灯灯箱（每只灯箱容积V最大时所装灯箱只数最少）？
（2）若材料成本2元/cm²，霓虹灯灯箱销售时以霓虹灯灯箱侧面积S（cm²）为准，售价为2.4元/cm²．试问每售出一个霓虹灯灯箱可获最大利润是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：

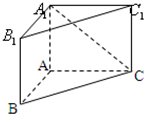如图，在直三棱柱ABC-A₁B₁C₁中，AB=1，AC=AA₁=

，BC=2
（Ⅰ）证明：AB⊥A₁C；
（Ⅱ）求直线BC₁与平面ACC₁A₁所成角的正切值．
（Ⅲ）求点A到平面A₁BC的距离．

查看答案和解析>>

科目：高中数学 来源： 题型：

已知|

|=1，|

|=4，

与

的夹角为60°，则

在

方向上的投影为

．

查看答案和解析>>

同步练习册答案