
【题目】已知各项是正数的数列![]() 的前n项和为
的前n项和为![]() .
.
(1)若![]() (nN*,n≥2),且
(nN*,n≥2),且![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)数列![]() 是公比为q(q>0, q1)的等比数列,且{an}的前n项积为
是公比为q(q>0, q1)的等比数列,且{an}的前n项积为![]() .若存在正整数k,对任意nN*,使得
.若存在正整数k,对任意nN*,使得![]() 为定值,求首项
为定值,求首项![]() 的值.
的值.
【答案】(1)①![]() ②
②![]() (2)
(2)![]()
【解析】
试题分析:(1)①当![]() 时,由
时,由![]() 可得
可得![]() 两式相减得
两式相减得![]() ,即
,即![]() ,
,![]() ,数列
,数列![]() 为等差数列,可得
为等差数列,可得![]() ,②由①知,
,②由①知,![]() ,所以
,所以![]() ,可得
,可得![]() 对一切
对一切![]() 恒成立,记
恒成立,记![]() ,,判断数列
,,判断数列![]() 的单调性,求出最大项,从而可得结果;(2)设
的单调性,求出最大项,从而可得结果;(2)设![]() (
(![]() ),
),![]() ,两边取常用对数,
,两边取常用对数,![]() . 令
. 令![]() ,则数列
,则数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列, 若
为公差的等差数列, 若![]() 为定值,令
为定值,令![]() ,化为.
,化为.![]() 对
对![]() 恒成立,问题等价于
恒成立,问题等价于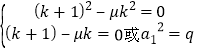 ,从而可得结果.
,从而可得结果.
试题解析:(1)①当![]() 时,由
时,由![]()
则![]()
两式相减得![]() ,即
,即![]() ,
,![]()
当![]() 时,
时,![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
所以![]() ,即数列
,即数列![]() 为等差数列,且首项
为等差数列,且首项![]() ,
,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
②由①知,![]() ,所以
,所以![]() ,
,
由题意可得![]() 对一切
对一切![]() 恒成立,
恒成立,
记![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(2)由题意,设![]() (
(![]() ),
),![]() ,两边取常用对数,
,两边取常用对数,![]() . 令
. 令![]() ,则数列
,则数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列, 若
为公差的等差数列, 若![]() 为定值,令
为定值,令![]() ,则
,则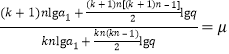 ,
,
即![]() 对
对![]() 恒成立,
恒成立,
因为![]() ,问题等价于
,问题等价于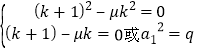
将![]() 代入
代入![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() 故
故![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆![]() 的离心率为
的离心率为![]() ,椭圆上动点
,椭圆上动点![]() 到一个焦点的距离的最小值为
到一个焦点的距离的最小值为![]() .
.
(1)求椭圆C的标准方程;
(2)已知过点![]() 的动直线l与椭圆C交于 A,B 两点,试判断以AB为直径的圆是否恒过定点,并说明理由.
的动直线l与椭圆C交于 A,B 两点,试判断以AB为直径的圆是否恒过定点,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100)六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:

(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某帆船中心比赛场馆区的海面上每天海浪高度y(米)可看作时间![]() (单位:小时)的函数,记作
(单位:小时)的函数,记作![]() ,经过长期观测,
,经过长期观测,![]() 的曲线可近似地看成是函数
的曲线可近似地看成是函数![]() ,下列是某日各时的浪高数据.
,下列是某日各时的浪高数据.
t/小时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y/米 |
| 1 |
| 1 |
| 1 |
| 1 |
|
(1)根据以上数据,求出![]() 的解析式;
的解析式;
(2)为保证安全比赛时的浪高不能高于![]() 米,则在一天中的哪些时间可以进行比赛.
米,则在一天中的哪些时间可以进行比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的![]() 人的得分(满分:
人的得分(满分:![]() 分)数据,统计结果如下表所示.
分)数据,统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)已知此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求
人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,环保部门为此次参加问卷调查的市民制定如下奖励方案.
(ⅰ)得分不低于![]() 的可以获赠
的可以获赠![]() 次随机话费,得分低于
次随机话费,得分低于![]() 的可以获赠
的可以获赠![]() 次随机话费;
次随机话费;
(ⅱ)每次赠送的随机话费和相应的概率如下表.
赠送的随机话费/元 |
|
|
概率 |
|
|
现市民甲要参加此次问卷调查,记![]() 为该市民参加问卷调查获赠的话费,求
为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com