
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的![]() 人的得分(满分:
人的得分(满分:![]() 分)数据,统计结果如下表所示.
分)数据,统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)已知此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求
人得分的平均值(同一组中的数据用该组区间的中点值为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,环保部门为此次参加问卷调查的市民制定如下奖励方案.
(ⅰ)得分不低于![]() 的可以获赠
的可以获赠![]() 次随机话费,得分低于
次随机话费,得分低于![]() 的可以获赠
的可以获赠![]() 次随机话费;
次随机话费;
(ⅱ)每次赠送的随机话费和相应的概率如下表.
赠送的随机话费/元 |
|
|
概率 |
|
|
现市民甲要参加此次问卷调查,记![]() 为该市民参加问卷调查获赠的话费,求
为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知各项是正数的数列![]() 的前n项和为
的前n项和为![]() .
.
(1)若![]() (nN*,n≥2),且
(nN*,n≥2),且![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)数列![]() 是公比为q(q>0, q1)的等比数列,且{an}的前n项积为
是公比为q(q>0, q1)的等比数列,且{an}的前n项积为![]() .若存在正整数k,对任意nN*,使得
.若存在正整数k,对任意nN*,使得![]() 为定值,求首项
为定值,求首项![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学的![]() 名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐
名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐![]() 名同学(乘同一辆车的
名同学(乘同一辆车的![]() 名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的
名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的![]() 名同学中恰有
名同学中恰有![]() 名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
名同学是来自于同一年级的乘坐方式共有_______种(有数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点A(2,6),且与直线l1: x+y-10=0相切于点B(6,4).
(1)求圆C的方程;
(2)过点P(6,24)的直线l2与圆C交于M,N两点,若△CMN为直角三角形,求直线l2的斜率;
(3)在直线l3: y=x-2上是否存在一点Q,过点Q向圆C引两切线,切点为E,F, 使△QEF为正三角形,若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.

(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,现有一组数据,将其绘制所得的茎叶图如图所示(其中茎为整数部分,叶为小数部分.例如:
,现有一组数据,将其绘制所得的茎叶图如图所示(其中茎为整数部分,叶为小数部分.例如:![]() 可记为
可记为![]() ,且上述数据的平均数为
,且上述数据的平均数为![]() .)
.)
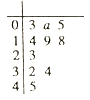
(Ⅰ)求茎叶图中数据![]() 的值;
的值;
(Ⅱ)现从茎叶图中小于![]() 的数据中任取两个数据分别替换
的数据中任取两个数据分别替换![]() 的值,求恰有一个数据使得函数没有零点的概率.
的值,求恰有一个数据使得函数没有零点的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com