
分析 利用等差中项的性质设这四个数分别为:x、8-d、8、8+d,利用等比中项的性质和条件列出方程组,求出方程组的解,在求出这四个数即可.
解答 解:依题意:后三个数成等差数列,和为24,
可设这四个数分别为:x、8-d、8、8+d,
因为前三个数和为14,前三个数成等比数列,
所以$\left\{\begin{array}{l}{x+16-d=14}\\{(8-d)^{2}=8x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=18}\\{d=20}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{d=4}\end{array}\right.$,
则这四个数分别为:18,-12,8,28或2,4,8,12.
点评 本题考查等差中项的性质,等比中项的性质的灵活运用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
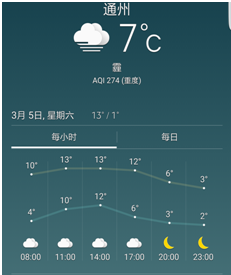 中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的最高气温,下面的折线代表可能出现的最低气温.
中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的最高气温,下面的折线代表可能出现的最低气温.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48种 | B. | 72种 | C. | 144种 | D. | 288种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com