
已知函数f(x)=(ax2+x-1)ex其中e是自然对数的底数a∈R.
(1)若a=1,求曲线f(x)在点(1,f(1))处的切线方程;
(2)若a<0,求f(x)的单调区间;
(3)若a=-1,函数f(x)的图象与函数g(x)=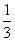 x3+
x3+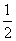 x2+m的图象有3个不同的交点,求实数m的取值范围.
x2+m的图象有3个不同的交点,求实数m的取值范围.
(1)a=1时,f(x)=(x2+x-1)ex,
所以f′(x)=(2x+1)ex+(x2+x-1)ex=(x2+3x)ex,
所以曲线f(x)在点(1,f(1))处的切线斜率为k=f′(1)=4e.
又因为f(1)=e,
所以所求切线方程为y-e=4e(x-1),即4ex-y-3e=0.
(2)f′(x)=(2ax+1)ex+(ax2+x-1)ex=[ax2+(2a+1)x]ex,
①若-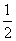 <a<0,当x<0或x>-
<a<0,当x<0或x>-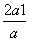 时,f′(x)<0;
时,f′(x)<0;
当0<x<-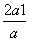 时,f′(x)>0.
时,f′(x)>0.
所以f(x)的单调递减区间为(-∞,0],[-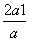 ,+∞);单调递增区间为[0,-
,+∞);单调递增区间为[0,-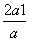 ].
].
②若a=-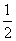 ,则f′(x)=-
,则f′(x)=-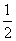 x2ex≤0,所以f(x)的单调递减区间为(-∞,+∞).
x2ex≤0,所以f(x)的单调递减区间为(-∞,+∞).
③若a<-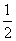 ,当x<-
,当x<-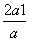 或x>0时,f′(x)<0;
或x>0时,f′(x)<0;
当-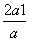 <x<0时,f′(x)>0.
<x<0时,f′(x)>0.



科目:高中数学 来源: 题型:
已知a、b、c为△ABC的三边长,若满足(a+b-c)(a+b+c)=ab,则∠C的大小为( )
A.60° B.90°
C.120° D.150°
查看答案和解析>>
科目:高中数学 来源: 题型:
某种电路开关闭合后,会出现红灯或绿灯闪烁,已知开关第一次闭合后出现红灯的概率是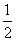 ,在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是
,在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是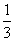 ,则两次闭合都出现红灯的概率为………………………………………( )
,则两次闭合都出现红灯的概率为………………………………………( )
A.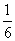 B.
B.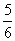 C.
C. 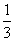 D.
D. 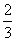
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com