
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数,
是参数,![]() 是大于0的常数).以坐标原点为极点,
是大于0的常数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)分别记直线![]() :
:![]() ,
,![]() 与圆
与圆![]() 、圆
、圆![]() 的异于原点的交点为
的异于原点的交点为![]() ,
,![]() ,若圆
,若圆![]() 与圆
与圆![]() 外切,试求实数
外切,试求实数![]() 的值及线段
的值及线段![]() 的长.
的长.
【答案】(1)圆![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 的直角坐标方程为
的直角坐标方程为![]() (2)
(2)![]() ,
,![]()
【解析】
(1)利用![]() 消去参数
消去参数![]() ,求得圆
,求得圆![]() 的普通方程,进而转化为极坐标方程.利用
的普通方程,进而转化为极坐标方程.利用![]() ,
,![]() 以及两角差的余弦公式,将圆
以及两角差的余弦公式,将圆![]() 的极坐标方程转化为直角坐标方程.
的极坐标方程转化为直角坐标方程.
(2)先求得两个圆的圆心和半径,利用两圆外切,圆心距等于两圆半径之和列方程,解方程求得![]() 的值.将
的值.将![]() 分别代入
分别代入![]() 的极坐标方程,利用
的极坐标方程,利用![]() 的几何意义,求得线段
的几何意义,求得线段![]() 的长.
的长.
(1)圆![]() :
:![]() (
(![]() 是参数)消去参数
是参数)消去参数![]() ,
,
得其普通方程为![]() ,
,
将![]() ,
,![]() 代入上式并化简,
代入上式并化简,
得圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
由圆![]() 的极坐标方程
的极坐标方程![]() ,得
,得![]() .
.
将![]() ,
,![]() ,
,![]() 代入上式,
代入上式,
得圆![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)由(1)知圆![]() 的圆心
的圆心![]() ,半径
,半径![]() ;圆
;圆![]() 的圆心
的圆心![]() ,半径
,半径![]() ,
,
![]() ,
,
∵圆![]() 与圆
与圆![]() 外切,
外切,
∴![]() ,解得
,解得![]() ,
,
即圆![]() 的极坐标方程为
的极坐标方程为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,得
,得![]() ,
,
故![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,…,
,…,![]() 为1,2,…,10的一个排列,则满足对任意正整数m,n,且
为1,2,…,10的一个排列,则满足对任意正整数m,n,且![]() ,都有
,都有![]() 成立的不同排列的个数为( )
成立的不同排列的个数为( )
A.512B.256C.255D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点. 设过点
为坐标原点. 设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点.
两点.
(1)求![]() 的方程;
的方程;
(2)是否存在这样的直线![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在,求出
,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 C 经过点 (2,3),它的渐近线方程为 y = ±![]() .椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
.椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
(1)求双曲线 C 和椭圆 C1 的方程;
(2)经过椭圆 C1 左焦点 F 的直线 l 与椭圆 C1 交于 A、B 两点,是否存在定点 D ,使得无论 AB 怎样运动,都有∠ADF = ∠BDF ?若存在,求出 D 点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=
=1(a>b>0)的左、右焦点,点A为椭圆C的左顶点,点B为椭圆C的上顶点,且|AB|=![]() ,△BF1F2为直角三角形.
,△BF1F2为直角三角形.
(1)求椭圆C的方程;
(2)设直线y=kx+2与椭圆交于P、Q两点,且OP⊥OQ,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的离心率
的离心率![]() ,左、右焦点分别是
,左、右焦点分别是![]() 、
、![]() ,且椭圆上一动点
,且椭圆上一动点![]() 到
到![]() 的最远距离为
的最远距离为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 以
以![]() 为直角时,求直线
为直角时,求直线![]() 的方程;
的方程;
(3)直线![]() 的斜率存在且不为0时,试问
的斜率存在且不为0时,试问![]() 轴上是否存在一点
轴上是否存在一点![]() 使得
使得![]() ,若存在,求出
,若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品自生产并投入市场以来,生产企业为确保产品质量,决定邀请第三方检测机构对产品进行质量检测,并依据质量指标![]() 来衡量产品的质量.当
来衡量产品的质量.当![]() 时,产品为优等品;当
时,产品为优等品;当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标
时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标![]() 的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
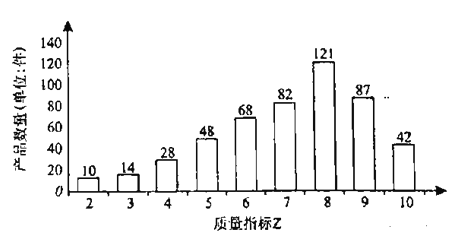
(1)从该企业生产的所有产品中随机抽取1件,求该产品为优等品的概率;
(2)现某人决定购买80件该产品.已知每件成本1000元,购买前,邀请第三方检测机构对要购买的80件产品进行抽样检测.买家、企业及第三方检测机构就检测方案达成以下协议:从80件产品中随机抽出4件产品进行检测,若检测出3件或4件为优等品,则按每件1600元购买,否则按每件1500元购买,每件产品的检测费用250元由企业承担.记企业的收益为![]() 元,求
元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)商场为推广此款产品,现面向意向客户推出“玩游戏,送大奖”活动.客户可根据抛硬币的结果,操控机器人在方格上行进,已知硬币出现正、反面的概率都是![]() ,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从
,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从![]() 到
到![]() ),若掷出反面,机器人向前移动两格(从
),若掷出反面,机器人向前移动两格(从![]() 到
到![]() ),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第
),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并解释此方案能否吸引顾客购买该款产品.
是等比数列,并解释此方案能否吸引顾客购买该款产品.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在
在![]() 上.
上.
(1) 求椭圆的方程;
(2) 设![]() 分别是椭圆
分别是椭圆![]() 的上、下焦点,过
的上、下焦点,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com