
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上的一个动点,点
上的一个动点,点![]()
![]() 分别在线段
分别在线段![]()
![]() 上,且满足
上,且满足![]() ,
,![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
【答案】(1)![]() .(2)存在,取值范围是
.(2)存在,取值范围是![]()
【解析】
(1)由![]() 知
知![]() 为线段
为线段![]() 的中点, 由
的中点, 由![]() 知
知![]() , 故点
, 故点![]() 为线段
为线段![]() 的垂直平分线上的一点,从而可得点
的垂直平分线上的一点,从而可得点![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为4的椭圆,由此可得其轨迹方程;
为焦点,长轴长为4的椭圆,由此可得其轨迹方程;
(2)点![]() 是椭圆的右焦点,设直线
是椭圆的右焦点,设直线![]() .与椭圆方程联立消去
.与椭圆方程联立消去![]() 得一元二次方程,设
得一元二次方程,设![]() ,则
,则![]() ,假设存在满足题意的点
,假设存在满足题意的点![]() ,则由对角线垂直即
,则由对角线垂直即![]() 可把
可把![]() 表示为
表示为![]() 的函数,结合不等式性质可得结论.
的函数,结合不等式性质可得结论.
(1)由![]() 知
知![]() 为线段
为线段![]() 的中点, 由
的中点, 由![]() 知
知![]() , 故点
, 故点![]() 为线段
为线段![]() 的垂直平分线上的一点,从而
的垂直平分线上的一点,从而![]() ,则有
,则有![]() ,
,
∴点![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为4的椭圆, ∵
为焦点,长轴长为4的椭圆, ∵![]() ∴
∴![]() ,∴点
,∴点![]() 的轨迹方程是
的轨迹方程是![]() .
.
(2)由(1)知点![]() 是椭圆的右焦点,设直线
是椭圆的右焦点,设直线![]() .
.
由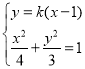 ,消去
,消去![]() 并整理,得到
并整理,得到![]() .
.
设![]() ,则
,则![]() ,从而
,从而![]()
假设存在满足题意的点![]() ,则
,则![]() ,
,
∵菱形的对角线互相垂直, ∴![]() ,
,
即![]()
又![]() ∴
∴![]()
即![]()
![]()
由![]() ,且
,且![]() ,
, 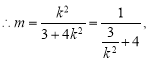
![]() ,
,
故存在满足题意的点![]() ,且
,且![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
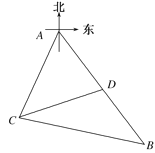
【题目】某观测站![]() 在目标
在目标![]() 的南偏西
的南偏西![]() 方向,从
方向,从![]() 出发有一条南偏东
出发有一条南偏东![]() 走向的公路,在
走向的公路,在![]() 处测得与
处测得与![]() 相距
相距![]() 的公路
的公路![]() 处有一个人正沿着此公路向
处有一个人正沿着此公路向![]() 走去,走
走去,走![]() 到达
到达![]() ,此时测得
,此时测得![]() 距离为
距离为![]() ,若此人必须在
,若此人必须在![]() 分钟内从
分钟内从![]() 处到达
处到达![]() 处,则此人的最小速度为( )
处,则此人的最小速度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 满足
满足![]() ,
,![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)求![]() 的最大项的值;
的最大项的值;
(3)数列![]() 满足
满足![]() ,问是否存在正整数k,使得
,问是否存在正整数k,使得![]()
![]() 成等差数列?若存在,求出k和m的值;若不存在,请说明理由.
成等差数列?若存在,求出k和m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】合肥一中、六中为了加强交流,增进友谊,两校准备举行一场足球赛,由合肥一中版画社的同学设计一幅矩形宣传画,要求画面面积为![]() ,画面的上、下各留
,画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.

(1)如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
(2)设画面的高与宽的比为![]() ,且
,且![]() ,求
,求![]() 为何值时,宣传画所用纸张面积最小?
为何值时,宣传画所用纸张面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆上的点,平面PAC⊥平面ABC,PA⊥AB.
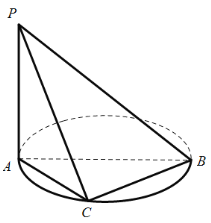
(1)求证:PA⊥平面ABC;
(2)若PA=AC=2,求点A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大位是我国明代著名的数学家,他的应用巨著《算法统综》中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节四升五,上梢四节三升八,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节竹的容积为
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x+![]() )+sin(x﹣
)+sin(x﹣![]() )+cosx.
)+cosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)在△ABC中,f(A)=![]() ,△ABC的面积为
,△ABC的面积为![]() ,AB=
,AB=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com