练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

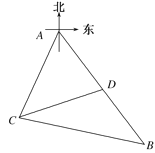
    【题目】某观测站在目标的南偏西方向，从出发有一条南偏东走向的公路，在处测得与相距的公路处有一个人正沿着此公路向走去，走到达，此时测得距离为，若此人必须在分钟内从处到达处，则此人的最小速度为(　　)

    A. B. C. D.

    【答案】B

    【解析】由已知得∠CAB＝25°＋35°＝60°，BC＝31，CD＝21，BD＝20，可得，那么，

    于是在△ABC中， ＝24，

    在△ABC中，BC2＝AC2＋AB2－2AC·ABcos60°，即312＝242＋AB2－24AB，解得AB＝35或AB＝－11(舍去)，因此AD＝AB－BD＝35－20＝15.

    故此人在D处距A处还有15 km，若此人必须在20分钟，即小时内从D处到达A处，则其最小速度为15÷＝45(km/h)．

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知点和．

    （）若， 是正方形一条边上的两个顶点，求这个正方形过顶点的两条边所在直线的方程；

    （）若， 是正方形一条对角线上的两个顶点，求这个正方形另外一条对角线所在直线的方程及其端点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知常数，函数．

    （1）讨论函数在区间上的单调性；

    （2）若存在两个极值点，且，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某观光海域AB段的长度为3百公里，一超级快艇在AB段航行，经过多次试验得到其每小时航行费用Q（单位：万元）与速度v（单位：百公里／小时）（0≤v≤3）的以下数据：

    0

    1

    2

    3

    0

    0.7

    1.6

    3.3

    为描述该超级快艇每小时航行费用Q与速度v的关系，现有以下三种函数模型供选择：Q＝av3＋bv2＋cv，Q＝0．5v＋a，Q＝klogav＋b．

    （1）试从中确定最符合实际的函数模型，并求出相应的函数解析式；

    （2）该超级快艇应以多大速度航行才能使AB段的航行费用最少？并求出最少航行费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数，

    （1）若函数为奇函数，求m的值；

    （2）若函数在上是增函数，求实数m的取值范围；

    （3）若函数在上的最小值为，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数有下述四个结论：

    ①是偶函数；②在区间单调递减；

    ③在有个零点；④的最大值为.

    其中所有正确结论的编号是（ ）

    A.①②④B.②④C.①④D.①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为、，过的直线交椭圆、两点，若的最大值为5，则b的值为（ ）

    A. 1 B. C. D. 2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{an}是等差数列，其前n项和为Sn ， {bn}是等比数列，且a1=b1=2，a4+b4=27，S4﹣b4=10．

    （1）求数列{an}与{bn}的通项公式；

    （2）记Tn=anb1+an﹣1b2+…+a1bn ， n∈N* ， 证明：Tn+12=﹣2an+10bn（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，点，点是圆上的一个动点，点分别在线段上，且满足，.

    （1）求点的轨迹方程；

    （2）过点作斜率为的直线与点的轨迹相交于两点，在轴上是否存在点，使得以为邻边的平行四边形是菱形？如果存在，求出的取值范围；如果不存在，说明理由.

    查看答案和解析>>

    同步练习册答案