
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 单调递减;
单调递减;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 的最大值为
的最大值为![]() .
.
其中所有正确结论的编号是( )
A.①②④B.②④C.①④D.①③
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() ,与
,与![]() 的交点为
的交点为![]() (异于原点),求
(异于原点),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资160万元,根据行业规定,每个城市至少要投资30万元,由前期市场调研可知:甲城市收益P与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() 单位:万元
单位:万元![]() 满足
满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() 单位:万元
单位:万元![]() ,两个城市的总收益为
,两个城市的总收益为![]() 单位:万元
单位:万元![]() .
.
(1)写出两个城市的总收益![]() 万元
万元![]() 关于甲城市的投入
关于甲城市的投入![]() 万元
万元![]() 的函数解析式,并求出当甲城市投资72万元时公司的总收益;
的函数解析式,并求出当甲城市投资72万元时公司的总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
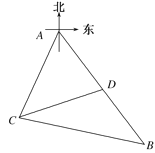
【题目】某观测站![]() 在目标
在目标![]() 的南偏西
的南偏西![]() 方向,从
方向,从![]() 出发有一条南偏东
出发有一条南偏东![]() 走向的公路,在
走向的公路,在![]() 处测得与
处测得与![]() 相距
相距![]() 的公路
的公路![]() 处有一个人正沿着此公路向
处有一个人正沿着此公路向![]() 走去,走
走去,走![]() 到达
到达![]() ,此时测得
,此时测得![]() 距离为
距离为![]() ,若此人必须在
,若此人必须在![]() 分钟内从
分钟内从![]() 处到达
处到达![]() 处,则此人的最小速度为( )
处,则此人的最小速度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A. 函数![]() 的一条对称轴是
的一条对称轴是![]()
B. 函数![]() 的一个对称中心是
的一个对称中心是![]()
C. 函数![]() 的一条对称轴是
的一条对称轴是![]()
D. 函数![]() 的一个对称中心是
的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人参加某电视台举办的答题闯关游戏,按照规则:每人从备选的10道题中一次性抽取3道题独立作答,至少答对2道题即闯关成功.已知10道备选题中,甲只能答对其中的6道题,乙答对每道题的概率都是![]() .
.
(Ⅰ)求甲闯关成功的概率;
(Ⅱ)设乙答对题目的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆上的点,平面PAC⊥平面ABC,PA⊥AB.
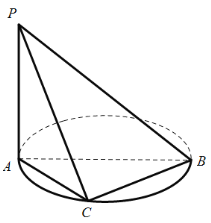
(1)求证:PA⊥平面ABC;
(2)若PA=AC=2,求点A到平面PBC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com