
分析 (1)利用奇函数的性质:f(-x)+f(x)=0,再利用对数的运算性质解出即可得出.
(2)由(1)可得:y=f(x)=loga($\sqrt{{x}^{2}+1}$+x),∴$\sqrt{{x}^{2}+1}+x$=ay,$\sqrt{{x}^{2}+1}$-x=a-y,解得x=$\frac{{a}^{y}-{a}^{-y}}{2}$,把x与y互换即可得出.
解答 解:(1)∵函数f(x)=loga($\sqrt{{x}^{2}+m}$+x)(a>0,a≠1)为奇函数.
∴f(-x)+f(x)=loga($\sqrt{{x}^{2}+m}$-x)+loga($\sqrt{{x}^{2}+m}$+x)=logam=0,解得m=1.
经过验证,满足题意,
∴m=1.
(2)由(1)可得:y=f(x)=loga($\sqrt{{x}^{2}+1}$+x),
∴$\sqrt{{x}^{2}+1}+x$=ay,$\sqrt{{x}^{2}+1}$-x=a-y,解得x=$\frac{{a}^{y}-{a}^{-y}}{2}$,
把x与y互换可得:y=$\frac{{a}^{x}-{a}^{-x}}{2}$,即f-1(x)=$\frac{{a}^{x}-{a}^{-x}}{2}$,即为原函数的反函数.
点评 本题考查了对数与指数函数的运算性质、反函数的求法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
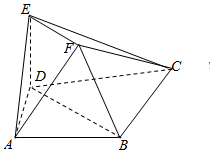 梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE=$\frac{1}{2}$BD,BD=BC=CD=$\sqrt{2}$AB=$\sqrt{2}$AD=2,DE⊥BC.
梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE=$\frac{1}{2}$BD,BD=BC=CD=$\sqrt{2}$AB=$\sqrt{2}$AD=2,DE⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个四面体的三视图都是等腰直角三角形,如图所示,则这个几何体四个表面中最小的一个表面面积是( )
一个四面体的三视图都是等腰直角三角形,如图所示,则这个几何体四个表面中最小的一个表面面积是( )| A. | $2\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 1 | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3),16 | B. | (-1,3),4 | C. | (1,-3),16 | D. | (1,-3),4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 0<x<5 | 5≤x<10 | 10≤x<15 | 15≤x≤20 |
| y=f(x) | -4 | 6 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
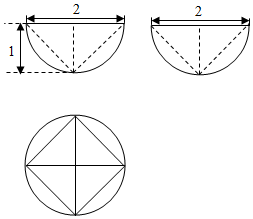 一个几何体的三视图如图所示,则这个几何体的体积为( )
一个几何体的三视图如图所示,则这个几何体的体积为( )| A. | $\frac{4π-2}{3}$ | B. | $\frac{4π-4}{3}$ | C. | $\frac{4π+2}{3}$ | D. | $\frac{2π-2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a、b∈R,则a-b=0⇒0⇒a=b,推出:若a,b∈C,则a-b=0⇒a=b | |
| B. | 若a、b∈R,则a2+b2=0⇒a=b=0,推出:若a、b∈C,则a2+b2=0⇒a=b=0 | |
| C. | 若a、b∈R,则a-b>0⇒a>b,推出:若a、b∈C,则a-b>0⇒a>b | |
| D. | 若x∈R,则|x|<1⇒-1<x<1,推出:若z∈C,则|x|<1⇒-1<x<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com