
 函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若$cos∠APB=-\frac{{\sqrt{5}}}{5}$,则ω的值为$\frac{π}{2}$.
函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若$cos∠APB=-\frac{{\sqrt{5}}}{5}$,则ω的值为$\frac{π}{2}$. 分析 由解析式求出函数的周期与最值,做出辅助线过p作PM⊥x轴于M,根据周期的大小看出直角三角形中直角边的长度,解出∠APM与∠BPM的正弦、余弦函数值,利用cos∠APB=-$\frac{\sqrt{5}}{5}$,求出ω的值.
解答 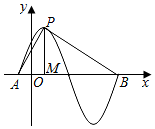 解:如图,函数y=sin(ωx+φ),
解:如图,函数y=sin(ωx+φ),
∴AB=T=$\frac{2π}{ω}$,最大值为1,
过P作PM⊥x轴于M,则AM是四分之一个周期,有AM=$\frac{π}{2ω}$,MB=$\frac{3π}{2ω}$,MP=1,
∴AP=$\sqrt{1+\frac{{π}^{2}}{4{ω}^{2}}}$,BP=$\sqrt{1+\frac{9{π}^{2}}{4{ω}^{2}}}$,
在直角三角形AMP中,有cos∠APM=$\frac{MP}{AP}$,sin∠APM=$\frac{AM}{AP}$,
在直角三角形BMP中cos∠BPM=$\frac{MP}{BP}$,sin∠BPM=$\frac{BM}{BP}$.
cos∠APB=cos(∠APM+∠BPM)=$\frac{MP}{AP}$•$\frac{MP}{BP}$-$\frac{AM}{AP}•\frac{BM}{BP}$=-$\frac{\sqrt{5}}{5}$.
∴$\frac{1}{\sqrt{1+\frac{{π}^{2}}{4{ω}^{2}}}•\sqrt{1+\frac{9{π}^{2}}{4{ω}^{2}}}}$$\frac{\frac{π}{2ω}•\frac{3π}{2ω}}{\sqrt{1+\frac{{π}^{2}}{4{ω}^{2}}}•\sqrt{1+\frac{9{π}^{2}}{4{ω}^{2}}}}$=-$\frac{\sqrt{5}}{5}$,
化简得:64ω4-160π2ω2+36π4=0,解得ω=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查三角函数的图象的应用与两角和的余弦函数公式的应用,本题解题的关键是看出函数的周期,把要求正弦的角放到直角三角形中,利用三角函数的定义得到结果,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 8或9 | B. | 9或10 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | -4 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
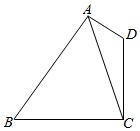 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 6 | 5 | 10 | 12 |
| y | 6 | 5 | 3 | 2 |
| A. | $\widehaty$=0.7x-2.3 | B. | $\widehaty$=-0.7x+10.3 | C. | $\widehaty$=-10.3x+0.7 | D. | $\widehaty$=10.3x-0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com