
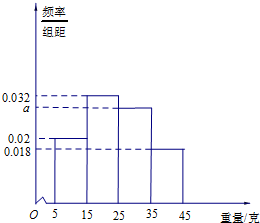
 测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.
测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.分析 (1)利用频率分布直方图,概率和为1,求解即可.
(2)结合频率分布直方图,利用分层抽样求解即可.
(3)求出重量在(5,15]内的尾数为ξ的可能值,求出概率得到分布列,然后求解期望即可.
解答 解:(1)由题意,得(0.02+0.032+x+0.018)×10=1,
解得x=0.03.…(2分)
(2)(25,35],(35,4]频数分别30个和18个,按分层抽样知 (35,45]中取$8×\frac{18}{48}$=3个…(4分)
(3)利用样本估计总体,马口鱼重量在(5,15]内性成熟的概率为0.2,则ξ:B(3,$\frac{1}{5}$).
ξ的取值为0,1,2,3,…(6分)
P(ξ=0)=${C}_{3}^{0}(\frac{4}{5})^{3}$=$\frac{64}{125}$,
P(ξ=1)=${C}_{3}^{1}×\frac{1}{5}×{(\frac{4}{5})}^{2}$=$\frac{48}{125}$,
P(ξ=2)=${C}_{3}^{2}×\frac{4}{5}×{(\frac{1}{5})}^{2}$=$\frac{12}{125}$,
P(ξ=3)=${C}_{3}^{3}{(\frac{1}{5})}^{3}$=$\frac{1}{125}$.…(10分)
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
点评 本题考查频率分布直方图的应用,分布列以及期望的求法,考查分析问题解决问题的能力.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 满意情况 | 不满意 | 比较满意 | 满意 | 非常满意 |
| 人数 | 200 | n | 2100 | 1000 |
| A. | $\frac{7}{15}$ | B. | $\frac{2}{5}$ | C. | $\frac{11}{15}$ | D. | $\frac{13}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com