
分析 (I)利用二倍角公式和两角和公式对函数解析式整理化简,进而求得函数的最小正周期;把图象过点代入函数解析式求得cosα的值,进而求得α.
(Ⅱ)利用正弦函数的图象和性质求得函数的单调增区间.
解答 解:(I)f(x)=2sin$({x-\frac{α}{2}})cos({x-\frac{α}{2}})+2\sqrt{3}{cos^2}({x-\frac{α}{2}})-\sqrt{3}$=sin(2x-α)+$\sqrt{3}$cos(2x-α)=2sin(2x-α+$\frac{π}{3}$)
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π,
∵函数图象过点$({\frac{π}{12},0})$,
∴2sin($\frac{π}{6}$-α+$\frac{π}{3}$)=0,
∴cosα=0,
∵α∈[0,π],
∴α=$\frac{π}{2}$.
(Ⅱ)由(I)知f(x)=2sin(2x-$\frac{π}{6}$),
由-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
得-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ,k∈Z,
∵$x∈[{0,\frac{π}{2}}]$,
∴f(x)的单调增区间为[0,$\frac{π}{3}$].
点评 本题主要考查了两角和公式,二倍角公式的应用,三角函数图象与性质的运用.考查学生对基础知识的掌握和熟练应用能力.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
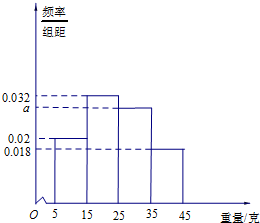 测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.
测量马口鱼性成熟时重量,从大量马口鱼中随机抽取100尾作为样本,测出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到重量样本的频率分布直方图,如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com