
���� ���ֱ�����й�������ʤ���ͳ�ʤ��ƽ�ĸ��ʺ��й�������ƽ�ͳ�ʤ�ĸ�����ͼ��ɣ�
���ó��й������п���ȡ�û��֣��ֱ�������ʼ��ɣ�
��� �⣺�����й�������ʤ���ͳ�ʤ��ƽ�ĸ���${p}_{1}=\frac{1}{2}��\frac{1}{3}+\frac{1}{2}��\frac{1}{3}=\frac{1}{3}$
�й�������ƽ�ͳ�ʤ�ĸ���${p}_{2}=\frac{1}{3}��\frac{1}{3}=\frac{1}{9}$��
���й��ӻ��ִ��ڿ������ӻ��ֵĸ���$p={p}_{1}+{p}_{2}=\frac{1}{3}+\frac{1}{9}=\frac{4}{9}$
����X����ȡ��ֵΪ18��19��20��21��22��24
P��X=18��=$\frac{1}{6}��\frac{1}{3}=\frac{1}{18}$��P��X=19��=$\frac{1}{3}��\frac{1}{3}+\frac{1}{6}��\frac{1}{3}=\frac{1}{6}$
P��X=20��=$\frac{1}{3}��\frac{1}{3}=\frac{1}{9}$��P��X=21��=$\frac{1}{2}��\frac{1}{3}+\frac{1}{6}��\frac{1}{3}=\frac{2}{9}$��
P��X=22��=$\frac{1}{2}��\frac{1}{3}+\frac{1}{3}��\frac{1}{3}=\frac{5}{18}$��P��X=24��=$\frac{1}{2}��\frac{1}{3}=\frac{1}{6}$
��X�ķֲ���Ϊ
| X | 18 | 19 | 20 | 21 | 22 | 24 |
| P | $\frac{1}{18}$ | $\frac{1}{6}$ | $\frac{1}{9}$ | $\frac{2}{9}$ | $\frac{5}{18}$ | $\frac{1}{6}$ |
���� ���⿼�����¼�������ĸ�����ⷽ�������ڳ������ͣ��ڿ��������������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
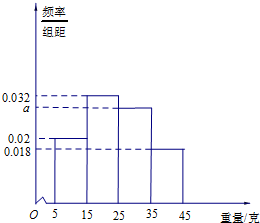 �����������Գ���ʱ�������Ӵ����������������ȡ100β��Ϊ������������ǵ���������λ���ˣ���������������Ϊ��5��15]����15��25]����25��35]����35��45]���ɴ˵õ�����������Ƶ�ʷֲ�ֱ��ͼ����ͼ��
�����������Գ���ʱ�������Ӵ����������������ȡ100β��Ϊ������������ǵ���������λ���ˣ���������������Ϊ��5��15]����15��25]����25��35]����35��45]���ɴ˵õ�����������Ƶ�ʷֲ�ֱ��ͼ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 1 | C�� | 2 | D�� | -9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ����������������ɵ��������ӵڶ�����ÿһ���е����־������������������֮�ͣ����һ�н���һ��������һ����ǰ100������������С�����ųɵ��У������һ�е�����101��298��
һ����������������ɵ��������ӵڶ�����ÿһ���е����־������������������֮�ͣ����һ�н���һ��������һ����ǰ100������������С�����ųɵ��У������һ�е�����101��298���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com