练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知△ABC中，cosA=$\frac{3}{5}，cosB=\frac{4}{5}$，BC=4，则AB=（　　）
    A．5B．4C．3D．2

    分析 先求得sinA和sinB的值，利用两角和公式求得sinC的值，最后利用正弦定理求得AB．

    解答 解：∵cosA=$\frac{3}{5}，cosB=\frac{4}{5}$，
    ∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{4}{5}$，sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{3}{5}$，
    ∴sinC=sin（A+B）=sinAcosB+cosAsinB=$\frac{4}{5}$×$\frac{4}{5}$+$\frac{3}{5}$×$\frac{3}{5}$=1，
    由正弦定理得$\frac{AB}{sinC}$=$\frac{BC}{sinA}$，即$\frac{AB}{1}$=$\frac{4}{\frac{4}{5}}$，
    ∴AB=5，
    故选A．

    点评 本题主要考查了正弦定理的运用和两角和公式的应用．注重了对学生基础公式灵活运用的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

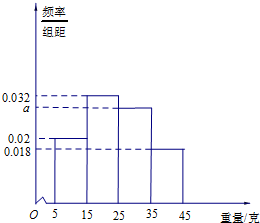    8．测量马口鱼性成熟时重量，从大量马口鱼中随机抽取100尾作为样本，测出它们的重量（单位：克），重量分组区间为（5，15]，（15，25]，（25，35]，（35，45]，由此得到重量样本的频率分布直方图，如图．
    （1）求a的值；
    （2）若重量在（25，35]，（35，45]中采用分层抽样方法抽出8尾作为特别实验，那么在（35，45]中需取出几尾？
    （3）从大量马口鱼中机抽取3尾，其中重量在（5，15]内的尾数为ξ，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．一个由若干行数字组成的数表，从第二行起，每一行中的数字均等于其肩上两个数字之和，最后一行仅有一个数，第一行是前100个正整数按从小到大排成的行，则最后一行的数是101×298．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知向量$\overrightarrow{a}$=（sinx，cosx），$\overrightarrow{b}$=（6sinx+cosx，7sinx-2cosx），设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$-2．
    （Ⅰ）求f（x）的最小正周期；
    （Ⅱ）在锐角△ABC中，角A、B、C的对边分别为a、b、c，f（A）=4且a=2，求角A及△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设函数f（x）=$\frac{1}{x+a}$+2lnx，其中a≠0，a∈R．
    （Ⅰ）讨论函数f（x）的单调性；
    （Ⅱ）设g（x）=$\frac{{x}^{2}+x-1}{{e}^{x}}$+m，求证：当a=-1，x∈（1，+∞）时，对任意的m＜$\frac{8}{5}$，总有f（x）＞g（x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知动点A在椭圆 C：$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$（a＞b＞0）上，动点B在直线 x=-2上，且满足 $\overrightarrow{OA}⊥\overrightarrow{OB}$（O为坐标原点），椭圆C上点 $M（\frac{{\sqrt{3}}}{2}，3）$到两焦点距离之和为 4$\sqrt{3}$
    （I）求椭圆C方程．
    （Ⅱ）求|AB|取最小值时点A的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=$\frac{alnx+b}{{e}^{x}}$（e是自然对数的底数，其中常数a，n满足a＞b，且a+b=1，函数y=f（x）的图象在点（1，f（1））处的切线斜率是2-$\frac{1}{a}$．
    （Ⅰ）求a，b的值；
    （Ⅱ）求函数f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知等差数列{an}的公差为d（d≠0），等比数列{bn}的公比为q（q＞0），且满足a1=b1=1，a2=b3，a6=b5．（1）求数列{an}的通项公式；
    （2）证明：对一切n∈N*，令bn=an•an+1，都有$\frac{1}{4}$≤$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$＜$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．求函数y=arctan（$\sqrt{2}$sinx-cosx）的值域．

    查看答案和解析>>

    同步练习册答案