
分析 由条件利用辅助角公式,正弦函数的值域求得($\sqrt{2}$sinx-cosx)∈[-$\sqrt{3}$,$\sqrt{3}$],再根据反正切函数的定义可得y=arctan($\sqrt{2}$sinx-cosx)的值域.
解答 解:由于 $\sqrt{2}$sinx-cosx=$\sqrt{3}$sin(x+θ),cosθ=$\frac{\sqrt{2}}{\sqrt{3}}$,sinθ=$\frac{1}{\sqrt{3}}$,
∴($\sqrt{2}$sinx-cosx)∈[-$\sqrt{3}$,$\sqrt{3}$].
再根据反正切函数的定义可得函数y=arctan($\sqrt{2}$sinx-cosx)∈[-$\frac{π}{3}$,$\frac{π}{3}$],
即函数y=arctan($\sqrt{2}$sinx-cosx)得值域为[-$\frac{π}{3}$,$\frac{π}{3}$].
点评 本题主要考查辅助角公式,正弦函数的值域,反正切函数的定义,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
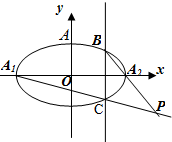 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额 | (0.200) | [200,400) | [400.600) | [600,800) | [800,1000] |
| 人数 | 10 | 25 | 35 | 30 | X |
| 消费金额 | (0.200) | [200,400) | [400.600) | [600,800) | [800.1000] |
| 人数 | 15 | 30 | 25 | Y | 5 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com