
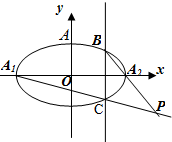
 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.分析 (1)由题设得 $\left\{\begin{array}{l}{a=2c}\\{a+a+2c=6}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$ 解得a,b,c.求得椭圆方程.
(2)分别设出直线A1C的方程和直线A2B的方程,两条直线相乘代入椭圆,证得结论.
(3)设直线l:$y-{y}_{0}=\frac{3{x}_{0}}{4{y}_{0}}(x-{x}_{0})$,结合第(2)问的结论得出相应结论
解答 解:(1)由题设得 $\left\{\begin{array}{l}{a=2c}\\{a+a+2c=6}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$ 解得:$a=2,b=\sqrt{3}$,c=1
故C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.(4分)
(2)证明:设B(x1,y1)则C(x1,-y1),A1(-2,0),A2(2,0)
∴直线A1C的方程为y=$\frac{-y1}{{x}_{1}+2}(x+2)$ ①(5分)
直线A2B的方程为y=$\frac{{y}_{1}}{{x}_{1}-2}(x-2)$ ②(6分)
①×②,得 ${y}^{2}=\frac{-{y}_{1}^{2}}{{x}_{1}^{2}-4}({x}^{2}-4)$ ③
$\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{3}=1$,∴$3{x}_{1}^{2}+4{y}_{1}^{2}=12$,∴${y}_{1}^{2}$=$\frac{-3({x}_{1}^{2}-4)}{4}$,
代入③得${y}^{2}=\frac{3}{4}({x}^{2}-4)$,即$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{3}=1$,(8分)
因为点P(x0,y0)是直线A1C与A2B的交点,所以$\frac{{x}_{0}^{2}}{4}-\frac{{y}_{0}^{2}}{3}=1$
即点P(x0,y0)在双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{3}=1$上(9分)
(3)设直线l:$y-{y}_{0}=\frac{3{x}_{0}}{4{y}_{0}}(x-{x}_{0})$(10分)
结合第(2)问的结论$\frac{{x}_{0}^{2}}{4}-\frac{{y}_{0}^{2}}{3}=1$,整理得:3x0x-4y0y-12=0(12分)
于是$d=\frac{12}{\sqrt{9{x}_{0}^{2}+16{y}_{0}^{2}}}=\frac{12}{\sqrt{21{x}_{0}^{2}-48}}$(14分)
$3{x}_{0}^{2}-{4}_{0}^{2}=12$且y0≠0∴${x}_{0}^{2}>4$∴$d=\frac{12}{\sqrt{21{x}_{0}^{2}-48}}∈(0,2)$
所以d的取值范围是 (0,2)(16分)
点评 本题主要考查直线与圆锥曲线的综合问题,有范围,有证明,综合性很强,难度很大,在高考中常作为压轴题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:填空题
 一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.
一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.
如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com