
 如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.
如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.分析 (1)∵抛物线的方程为y2=2px,∴得到直线l的方程,再利用点Q在线段OF的垂直平分线上的条件得出结论.
(2)设A(x1,y1),B(x2,y2),由已知得,$\frac{4}{{y}_{1}+{y}_{2}}=-\frac{2}{{y}_{0}}$⇒y1+y2=-2y0,因为点A,B,P均在抛物线y2=4x上,所以有${x}_{1}=\frac{{y}_{1}^{2}}{4},{x}_{2}=\frac{{y}_{2}^{2}}{4}$,${x}_{0}=\frac{{y}_{0}^{2}}{4}$,把它们分别代入即可.
解答 解:(1)∵抛物线的方程为y2=2px,∴直线l的方程为$x=-\frac{p}{2}$…(1分)
又∵点Q在线段OF的垂直平分线上,且F为抛物线y2=2px的焦点,
∴点Q的横坐标为$\frac{p}{4}$.…(2分)
又∵点Q到抛物线的准线l的距离为$\frac{3}{2}$,∴$\frac{3}{4}p=\frac{3}{2}$,即p=2.
∴抛物线的方程为y2=4x.…(5分)
(2)设A(x1,y1),B(x2,y2),则${k}_{AB}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$
又因为点A,B均在抛物线y2=4x上,所以有${x}_{1}=\frac{{y}_{1}^{2}}{4},{x}_{2}=\frac{{y}_{2}^{2}}{4}$,
所以${k}_{AB}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}=\frac{{y}_{2}-{y}_{1}}{\frac{{y}_{2}^{2}}{4}-\frac{{y}_{1}^{2}}{4}}=\frac{4}{{y}_{1}+{y}_{2}}$,
故由已知得,$\frac{4}{{y}_{1}+{y}_{2}}=-\frac{2}{{y}_{0}}$⇒y1+y2=-2y0(*)…(7分)
又由已知易知x1≠x0,x2≠x0,所以有${k}_{PA}=\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}},{k}_{PB}=\frac{{y}_{2}-{y}_{0}}{{x}_{2}-{x}_{0}}$
从而有${k}_{PA}+{k}_{PB}=\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}}+\frac{{y}_{2}-{y}_{0}}{{x}_{2}-{x}_{0}}$,(**)…(8分)
又因为点A,B,P均在抛物线y2=4x上,所以有${x}_{1}=\frac{{y}_{1}^{2}}{4},{x}_{2}=\frac{{y}_{2}^{2}}{4}$,${x}_{0}=\frac{{y}_{0}^{2}}{4}$,把它们分别代入(**)式,并化简可得:
${k}_{PA}+{k}_{PB}=\frac{4}{{y}_{1}+{y}_{0}}+\frac{4}{{y}_{2}+{y}_{0}}$=$\frac{4({y}_{2}+{y}_{0})+4({y}_{1}+{y}_{0})}{({y}_{1}+{y}_{0})({y}_{2}+{y}_{0})}=\frac{4({y}_{1}+{y}_{2}+2{y}_{0})}{({y}_{1}+{y}_{0})({y}_{2}+{y}_{0})}$…(10分)
把(*)代入,可得${k}_{PA}+{k}_{PB}=\frac{4({y}_{1}+{y}_{2}+2{y}_{0})}{({y}_{1}+{y}_{0})({y}_{2}+{y}_{0})}=0$
故直线PA、PB的倾斜角互补…(12分)
点评 本题主要考查直线与圆锥曲线的综合问题,计算量很大,属于难题,高考中常作压轴题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则A=2,ω=2,F($\frac{π}{3}$)=1.
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则A=2,ω=2,F($\frac{π}{3}$)=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
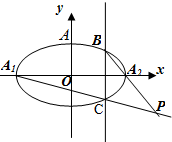 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
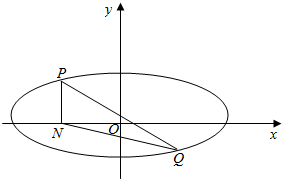 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com