
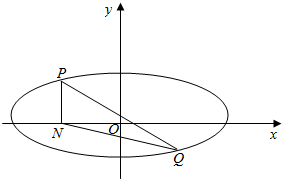
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).分析 (Ⅰ)依题得 $\frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{3}}}{2}$且b=1,∴a2=4,求得椭圆的标准方程=.
(Ⅱ)依题得,P(x0,y0),Q(-x0,-y0),N(x0,0),由面积公式求得,再利用均值不等式得到结论.
解答 解:(Ⅰ)解:依题得 $\frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{3}}}{2}$且b=1,∴a2=4,…(4分)
所以椭圆的标准方程为$\frac{x^2}{4}+{y^2}=1$…(5分)
(Ⅱ)依题得,P(x0,y0),Q(-x0,-y0),N(x0,0),…(6分)
又因为${S_{△PQN}}={S_{△PON}}+{S_{△ONQ}}=\frac{1}{2}|{ON}||{{y_p}-{y_Q}}|=|{{x_0}{y_0}}|$…(9分)
又∵$1=\frac{{{x_0}^2}}{4}+{y_0}^2≥2\sqrt{\frac{{{x_0}^2}}{4}•{y_0}^2}=|{{x_0}•{y_0}}|$…(12分)
即|x0•y0|≤1当且仅当$|{x_0}|=\sqrt{2}$,$|{y_0}|=\frac{{\sqrt{2}}}{2}$时等号成立∴△PQN的面积最大值为1…(14分)
点评 本题主要考查椭圆中得三角形面积最值问题,属于常考题型,中档题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 (1)求⊙P的半径(用θ表示);
(1)求⊙P的半径(用θ表示);查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.
如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
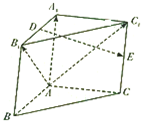 如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
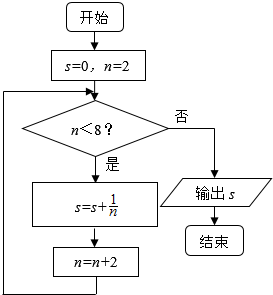 如图所示,程序框图的输出结果是( )
如图所示,程序框图的输出结果是( )| A. | $\frac{1}{16}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com