Question

【题目】已知函数f（x）=|x+2|+|x+a|（a∈R）．
（Ⅰ）若a=5，求函数f（x）的最小值，并写出此时x的取值集合；
（Ⅱ）若f（x）≥3恒成立，求a的取值范围．

Answer 1

【答案】解：（Ⅰ）若a=5，f（x）=|x+2|+|x+5|= ．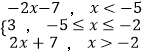
其图象如图：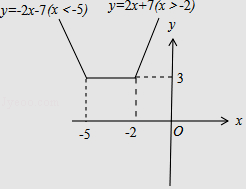

∴f（x）的最小值为3，使f（x）取得最小值的x的集合为{x|﹣5≤x≤﹣2}；
（Ⅱ）f（x）=|x+2|+|x+a|=|x﹣（﹣2）|+|x﹣（﹣a）|，
由绝对值的几何意义可知，f（x）为数轴上动点x与两个定点﹣2、﹣a的距离的和，
如图：

当动点x与﹣2重合时，|x﹣（﹣2）|最小为0，要使f（x）≥3恒成立，
则|﹣2﹣（﹣a）|≥3，即|a﹣2|≥3，得a﹣2≤﹣3或a﹣2≥3，
∴a≤﹣1或a≥5
【解析】（Ⅰ）写出分段函数，画图得答案；（Ⅱ）由绝对值的几何意义，把f（x）≥3恒成立转化为关于a的含有绝对值的不等式求解．