
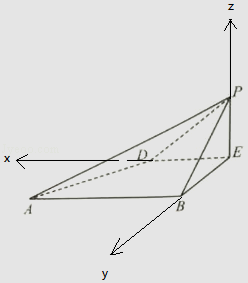
【题目】已知边长为2的菱形ABCD中,∠BCD=60°,E为DC的中点,如图1所示,将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,如图2所示. 
(Ⅰ)求证:△PAB为直角三角形;
(Ⅱ)求二面角A﹣PD﹣E的余弦值.
【答案】证明:(Ⅰ)∵边长为2的菱形ABCD中,∠BCD=60°,E为DC的中点,如图1所示, ∴BE⊥DC,AB∥CD,∴AB⊥BE,∴∠ABE=90°,
∵将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,如图2所示.
在翻折过程中,∠ABE=90°不变,
∴在△ABP中,∠ABP=90°,
∴△PAB为直角三角形.
解:(Ⅱ)由(Ⅰ)得∠BED=∠ABE=90°,∴DE⊥BE,
以E为原点,ED为x轴,EB为y轴,EP为z轴,建立空间直角坐标系,
A(2, ![]() ,0),P(0,0,1),D(1,0,0),E(0,0,0),
,0),P(0,0,1),D(1,0,0),E(0,0,0),![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(1,
=(1, ![]() ,0),
,0), ![]() =(0,0,1),
=(0,0,1), ![]() =(1,0,0),
=(1,0,0),
设平面ADP的法向量 ![]() =(x,y,z),
=(x,y,z),
则 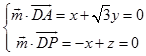 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
平面PDE的法向量 ![]() =(1,0,0),
=(1,0,0),
设二面角A﹣PD﹣E的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴二面角A﹣PD﹣E的余弦值为 ![]() .
.
【解析】(Ⅰ)推导出BE⊥DC,AB∥CD,从而AB⊥BE,进而∠ABE=90°,将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,在翻折过程中,∠ABE=90°不变,由此能证明△PAB为直角三角形.(Ⅱ)以E为原点,ED为x轴,EB为y轴,EP为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣PD﹣E的余弦值.
【考点精析】利用直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】若1![]()
A. logab>logba B. |logab+logba|>2
C. (logba)2<1 D. |logab|+|logba|>|logab+logba|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|+|x+a|(a∈R).
(Ⅰ)若a=5,求函数f(x)的最小值,并写出此时x的取值集合;
(Ⅱ)若f(x)≥3恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两名同学的数学学习情况,对他们的![]() 次数学测试成绩(满分
次数学测试成绩(满分![]() 分)进行统计,作出如下的茎叶图,其中
分)进行统计,作出如下的茎叶图,其中![]() 处的数字模糊不清,已知甲同学成绩的中位数是
处的数字模糊不清,已知甲同学成绩的中位数是![]() ,乙同学成绩的平均分是
,乙同学成绩的平均分是![]() 分.
分.

(1)求![]() 和
和![]() 的值;
的值;
(2)现从成绩在![]() 之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,且过点M(4,1). (Ⅰ)求椭圆C的方程;
,且过点M(4,1). (Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=x+m(m≠﹣3)与椭圆C交于P,Q两点,记直线MP,MQ的斜率分别为k1 , k2 , 试探究k1+k2是否为定值.若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为![]() ,
,![]() ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() .若用每天
.若用每天![]() 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作![]() .
.
(1)令![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求![]() 的表达式,并规定当
的表达式,并规定当![]() 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当![]() 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com