
为了保证信息安全,传输必须使用加密方式,有一种方式其加密、解密原理如下:
明文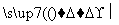 密文
密文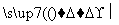 密文
密文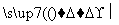 明文
明文
已知加密为y=ax-2(x为明文、y为密文),如果明文“3”通过加密后得到密文为“6”,再发送,接收方通过解密得到明文“3”,若接收方接到密文为“14”,则原发的明文是________.
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
设a=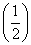 0.5,b=0.30.5,c=log0.30.2,则a、b、c的大小关系是( )
0.5,b=0.30.5,c=log0.30.2,则a、b、c的大小关系是( )
A.a>b>c B.a<b<c
C.b<a<c D.a<c<b
查看答案和解析>>
科目:高中数学 来源: 题型:
放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变.假设在放射性同位素铯137的衰变过程中,其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M02- ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是-10ln 2(太贝克/年),则M(60)=( ).
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是-10ln 2(太贝克/年),则M(60)=( ).
A.5太贝克 B.75ln 2太贝克
C.150ln 2太贝克 D.150太贝克
查看答案和解析>>
科目:高中数学 来源: 题型:
某学校要建造一个面积为10 000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
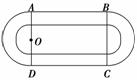
(1)设半圆的半径OA=r(米),设建立塑胶跑道面积S与r的函数关系S(r);
(2)由于条件限制r∈[30,40],问当r取何值时,运动场造价最低?最低造价为多少?(精确到元)
查看答案和解析>>
科目:高中数学 来源: 题型:
等比数列{an}中,a1=2,a8=4,函数f(x)=x(x-a1)(x-a2)…(x-a8),则f′(0)=( ).
A.26 B.29 C.212 D.215
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com