
【题目】在直角坐标系xOy中,曲线 ![]() (t为参数,t∈R),曲线
(t为参数,t∈R),曲线 ![]() (θ为参数,θ∈[0,2π]).
(θ为参数,θ∈[0,2π]).
(Ⅰ)以O为极点,x轴正半轴为极轴,取相同的长度单位建立极坐标系,求曲线C2的极坐标方程;
(Ⅱ)若曲线C1与曲线C2相交于点A、B,求|AB|.
【答案】解(Ⅰ)由 ![]() 消去参数后得到其普通方程为x2﹣4x+y2=0,
消去参数后得到其普通方程为x2﹣4x+y2=0,
把x=ρcosθ,y=ρsinθ代入可得ρ=4cosθ.
∴曲线C2的极坐标方程为ρ=4cosθ.
(Ⅱ)由 ![]() 消去参数后得到其普通方程为x+y﹣3=0,
消去参数后得到其普通方程为x+y﹣3=0,
由曲线C2可知:以(2,0)为圆心,以2为半径的圆.
那么:圆心到直线C1的距离为 ![]() ,
,
∴弦长 ![]() .
.
解法2:把 ![]() 代入x2﹣4x+y2=0得8t2﹣12t+1=0,
代入x2﹣4x+y2=0得8t2﹣12t+1=0,
则有: ![]() ,
, ![]() ,
,
则 ![]() ,
,
根据直线方程的参数几何意义知 ![]()
【解析】(Ⅰ)消去参数后得到其普通方程,把x=ρcosθ,y=ρsinθ代入可得曲线C2的极坐标方程;(Ⅱ)法一:利用弦长公式直接求解,利用参数的几何意义求解.法二、运用直线的参数方程求解.


科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖方法是:从装有2个红球A1 ,A2和1个白球B的甲箱与装有2个红球a1 ,a2和2个白球b1,b2的乙箱中,各随机摸出1个球.若摸出的2个球都是红球则中奖,否则不中奖.
(1)用球的标号列出所有可能的摸出结果;
(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率.你认为正确吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)设 ,计算
,计算![]() 的导数.
的导数.
【答案】(1)![]() .(2)
.(2) .
.
【解析】试题分析:(1)由导数的基本定义就出斜率,根据点斜式写出切线方程![]() ;(2)
;(2)![]() ,
,  .
.
试题解析:
(1)![]() ,则
,则![]() ,
,
又![]() ,∴所求切线方程为
,∴所求切线方程为![]() ,即
,即![]() .
.
(2)![]() ,
,  .
.
【题型】解答题
【结束】
18
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高一学生有800人,试估计该校高一学生参加社区服务的次数在区间![]() 内的人数.
内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列条件求圆的方程.
(![]() )
)![]() ,
, ![]() ,
, ![]() ,三角形
,三角形![]() 的外接圆.
的外接圆.
(![]() )圆心在直线
)圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() .
.
(![]() )与
)与![]() 轴相切,圆心在直线
轴相切,圆心在直线![]() 上,且被直线
上,且被直线![]() 截得的弦长为
截得的弦长为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为1的动圆与定圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是( )
A. (x-5)2+(y+7)2=25
B. (x-5)2+(y+7)2=3或(x-5)2+(y+7)2=15
C. (x-5)2+(y+7)2=9
D. (x-5)2+(y+7)2=25或(x-5)2+(y+7)2=9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电力公司为了制定节电方案,需要了解居民用电情况.通过随机抽样,电力公司获得了50户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).


(1)求a,b的值;
(2)为了解用电量较大的用户用电情况,在第5、6两组用分层抽样的方法选取5户 .
①求第5、6两组各取多少户?
②若再从这5户中随机选出2户进行入户了解用电情况,求这2户中至少有一户月平均用电量在[1000,1200]范围内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 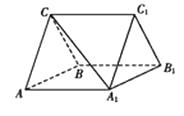
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C= ![]() ,求二面角B﹣AC﹣A1的余弦值.
,求二面角B﹣AC﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
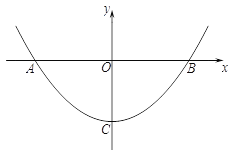
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,且位于x轴下方.
(1)如下图,若P(1,-3)、B(4,0),① 求该抛物线的解析式;② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如下图,在图中的抛物线解析式不变的条件下,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,OE+OF是否为定值?若是,试求出该定值;若不是,请说明理由.
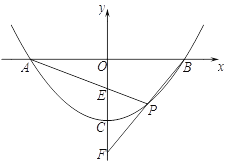
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com