
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
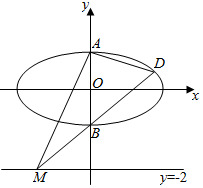 已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{b^2}$=1(2>b>0)的上、下顶点分别为A、B,过点B的直线与椭圆交于另一点D,与直线y=-2交于点M.
已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{b^2}$=1(2>b>0)的上、下顶点分别为A、B,过点B的直线与椭圆交于另一点D,与直线y=-2交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°.
已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
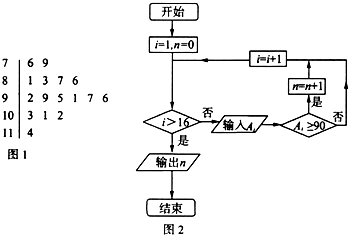 图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A1,A2,…,A16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )
图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次是A1,A2,…,A16,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )| A. | 6 | B. | 7 | C. | 10 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com